
- ავტორი Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:37.
- ბოლოს შეცვლილი 2025-06-01 05:04.
ა სრულად დაკავშირებული ქსელი, სრული ტოპოლოგია , ან სრული ბადე ტოპოლოგია არის ქსელი ტოპოლოგია რომელშიც არის პირდაპირი კავშირი ყველა წყვილ კვანძს შორის.
ამასთან დაკავშირებით, რა არის ხაზის ტოპოლოგია?
Ში ხაზის ტოპოლოგია -ასევე ცნობილია როგორც daisy-chaining ან bus ტოპოლოგია - მასპინძელი პირდაპირ კავშირშია ყველა კვანძთან ერთი ავტობუსის საშუალებით ხაზი . თუ სასურველია, სტანდარტული Ethernet მოწყობილობა ან გადამრთველი შეიძლება დაემატოს ჯაჭვის ბოლოს და გამოიყენოს ჩვეულებრივად.
გარდა ამისა, რა არის მთავარი განსხვავება სრულად დაკავშირებულ ქსელის ტოპოლოგიასა და ქსელის ქსელის ტოპოლოგიას შორის? ა სრულად დაკავშირებული ქსელის ტოპოლოგია აქვს ყველა კვანძი დაკავშირებულია ყველა სხვა კვანძზე. თუ თქვენ იცით გრაფიკის თეორია, მაშინ ის ჰგავს ა სრულად დაკავშირებული გრაფიკი, სადაც ყველა კვანძია დაკავშირებულია ყველა სხვა კვანძზე. მეორეს მხრივ, ნაწილობრივ დაკავშირებული ქსელის ტოპოლოგია არ აქვს ყველა კვანძი დაკავშირებულია ერთმანეთს.
ასევე, რა არის ტოპოლოგია და ტოპოლოგიის ტიპი?
ქსელში კომპიუტერებს შორის ურთიერთკავშირების განლაგების სქემას ეწოდება ქსელი ტოპოლოგია . ქსელი ტოპოლოგია ილუსტრირებულია ამ კვანძების და მათი კავშირების ჩვენებით კაბელების გამოყენებით. არსებობს მთელი რიგი სხვადასხვა ტიპები ქსელის ტოპოლოგიები , მათ შორის წერტილიდან წერტილამდე, ავტობუსი, ვარსკვლავი, ბეჭედი, ბადე, ხე და ჰიბრიდი.
რა არის 5 ქსელის ტოპოლოგია?
კომპიუტერული ქსელის ტოპოლოგია - ბადე, ვარსკვლავი, ავტობუსი, რგოლი და ჰიბრიდი
- კომპიუტერულ ქსელებში ტოპოლოგიის ხუთი ტიპი არსებობს:
- ქსელის ტოპოლოგიაში თითოეული მოწყობილობა დაკავშირებულია ქსელში არსებულ ყველა სხვა მოწყობილობასთან გამოყოფილი წერტილიდან წერტილამდე ბმულის საშუალებით.
- ვარსკვლავის ტოპოლოგიაში, ქსელში თითოეული მოწყობილობა დაკავშირებულია ცენტრალურ მოწყობილობასთან, რომელსაც ჰაბს უწოდებენ.
გირჩევთ:
რომელი მთის ქედის გადის სრულად?

ანდების მთები
აქვს თუ არა ფორმულ ფაილებს ტოპოლოგია?
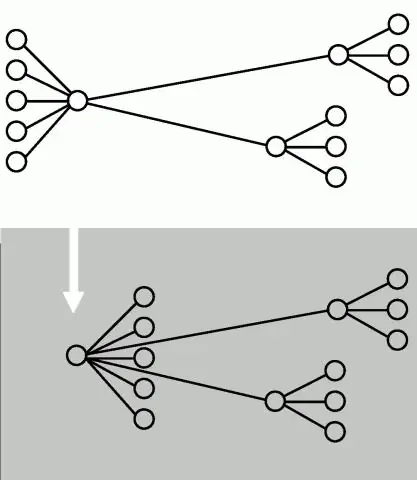
Shapefiles დაინერგა ArcView 2-ის გამოშვებით 1990-იანი წლების დასაწყისში. Shapefile არის არატოპოლოგიური მონაცემთა სტრუქტურა, რომელიც არ ინახავს ცალსახად ტოპოლოგიურ ურთიერთობებს. თუმცა, სხვა მარტივი გრაფიკული მონაცემთა სტრუქტურებისგან განსხვავებით, shapefile პოლიგონები წარმოდგენილია ერთი ან მეტი რგოლებით
არის თუ არა უჯრედის მემბრანა სრულად გამტარი?

გამტარი მემბრანის უჯრედის კედლები უზრუნველყოფს მცენარის უჯრედების მხარდაჭერას და დაცვას. ისინი სრულად არიან გამტარი წყლის, მოლეკულებისა და ცილების მიმართ. ეს საშუალებას აძლევს წყლისა და საკვები ნივთიერებების თავისუფლად გაცვლას მცენარეთა უჯრედებს შორის
რა არის ტოპოლოგია GIS PDF-ში?
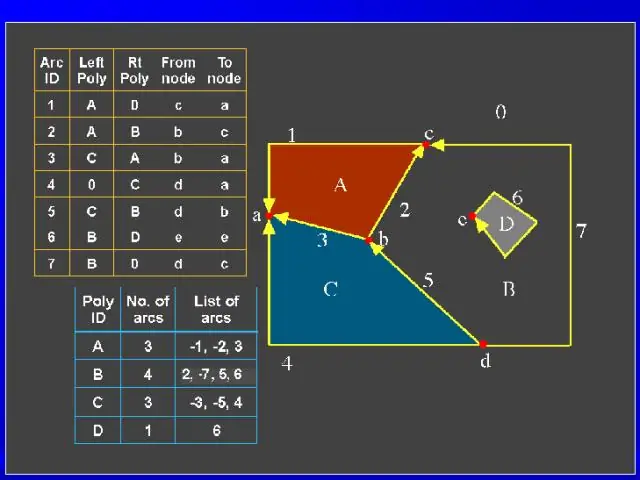
GIS-ში ტოპოლოგია განისაზღვრა, როგორც „მეცნიერება და მათემატიკური ურთიერთობები, რომლებიც გამოიყენება. დაადასტურეთ ერთეულების ვექტორული გეომეტრია და ოპერაციების სერია, როგორიცაა ქსელის ანალიზი და. სამეზობლო“[2]. ტოპოლოგიის წერტილები იძლევა სივრცითი ანალიზს, როგორიცაა ბუფერი, რათა დადგინდეს რა ობიექტებია ინა
როგორ მუშაობს ავტობუსის ქსელის ტოპოლოგია?
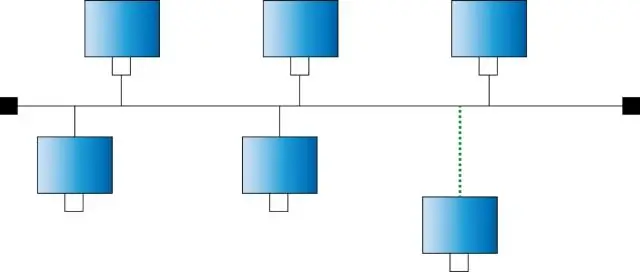
ავტობუსის ტოპოლოგია იყენებს ერთ მთავარ კაბელს, რომელსაც ყველა კვანძი პირდაპირ უკავშირდება. მთავარი კაბელი მოქმედებს როგორც ხერხემალი ქსელისთვის. ერთ-ერთი კომპიუტერი ქსელში, როგორც წესი, მოქმედებს როგორც კომპიუტერის სერვერი. ავტობუსის ტოპოლოგიის პირველი უპირატესობა ის არის, რომ ადვილია კომპიუტერის ან პერიფერიული მოწყობილობის დაკავშირება
