
- ავტორი Miles Stephen [email protected].
- Public 2023-12-15 23:37.
- ბოლოს შეცვლილი 2025-01-22 17:03.
დომენი შეზღუდვები ა რაციონალური ფუნქცია შეიძლება განისაზღვროს მნიშვნელის ნულის ტოლი დაყენებით და ამოხსნით. x-მნიშვნელობები, რომლებშიც მნიშვნელი უდრის ნულს არიან სინგულარობას უწოდებენ და არიან არა დომენში ფუნქცია.
ანალოგიურად, რატომ არის რაციონალური ფუნქციები მნიშვნელოვანი?
მნიშვნელობა. " რაციონალური ფუნქცია " ასე ჰქვია ა ფუნქცია რომელიც შეიძლება წარმოდგენილი იყოს მრავალწევრების კოეფიციენტად, ისევე როგორც ა რაციონალური რიცხვი არის რიცხვი, რომელიც შეიძლება გამოისახოს როგორც მთელი რიცხვების კოეფიციენტი. რაციონალური ფუნქციები მიწოდება მნიშვნელოვანი მაგალითები და ბუნებრივად გვხვდება მრავალ კონტექსტში.
ანალოგიურად, აქვთ თუ არა რაციონალურ ფუნქციებს გარდამტეხი წერტილები? 4 რეზიუმე. n ხარისხის მრავალწევრი აქვს მაქსიმუმ n რეალური ნული და n−1 გარდამტეხი წერტილები . ა რაციონალური ფუნქცია არის ფუნქცია ფორმის f(x)=P(x)Q(x), f (x) = P (x) Q (x), სადაც P(x) და Q(x) არიან ორივე მრავალწევრი.
ასევე კითხვაა, რა არის რაციონალური ფუნქციის მაგალითი?
მაგალითები დან რაციონალური ფუნქციები The ფუნქცია R(x) = (x^2 + 4x - 1) / (3x^2 - 9x + 2) არის რაციონალური ფუნქცია ვინაიდან მრიცხველი, x^2 + 4x - 1, არის მრავალწევრი და მნიშვნელი, 3x^2 - 9x + 2 ასევე მრავალწევრია.
რა არის რაციონალური ფუნქციების მახასიათებლები?
ორი მნიშვნელოვანი მახასიათებლები ნებისმიერი რაციონალური ფუნქცია r(x)=p(x)q(x) r (x) = p (x) q (x) არის ნებისმიერი ნული და ვერტიკალური ასიმპტოტები ფუნქცია შეიძლება ჰქონდეს. ეს ასპექტები ა რაციონალური ფუნქცია მჭიდროდ არის დაკავშირებული იქ, სადაც მრიცხველი და მნიშვნელი, შესაბამისად, ნულია.
გირჩევთ:
რა არის თვისებების თეორიის შეზღუდვები?

თვისებების თეორიების კიდევ ერთი შეზღუდვა არის ის, რომ ისინი საჭიროებენ პერსონალურ დაკვირვებებს ან სუბიექტურ თვითშეფასებას, რაც მოითხოვს ინდივიდებს იყოს საკმარისად ინტროსპექტიული, რათა იცოდნენ საკუთარი ქცევა. მიუხედავად იმისა, რომ თვისებების თეორიები გვაწვდიან ინფორმაციას იმის შესახებ, თუ როგორ შეიძლება მოიქცნენ ინდივიდები, ისინი არ ხსნიან რატომ შეიძლება მოიქცნენ ასე
რა შეზღუდვები აქვს ტიპოლოგიურ მიდგომას?

რა არის ტიპოლოგიური მიდგომის დადებითი და უარყოფითი მხარეები? უპირატესობები: აღწერითი, გამოსადეგია განათლებისთვის/თეორიტიკისთვის, ავლენს ინდივიდუალურ განსხვავებებს. ნაკლოვანებები: უგულებელყოფს მსგავსებებს, არ არის აუცილებელი ქცევის წინასწარმეტყველება, მცირე ფსიქომეტრიული სარგებელი
როგორ გამოვიყენო განზომილებიანი შეზღუდვები AutoCAD-ში?
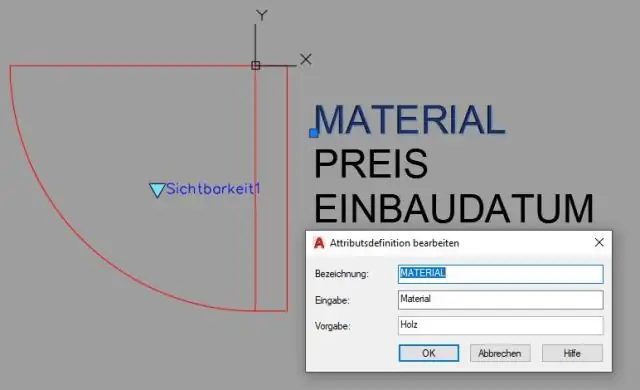
ეს ნაბიჯები წარმოგიდგენთ განზომილებიანი შეზღუდვების მარტივ მაგალითს: დაიწყეთ ახალი ნახაზი და აქციეთ ლენტის პარამეტრული ჩანართი მიმდინარე. ჩართეთ შესაბამისი ზუსტი ხატვის დამხმარე საშუალებები სტატუსის ზოლზე, როგორიცაა Snap, Ortho და Osnap. დახაზეთ საკმაოდ ზუსტი გეომეტრია ზუსტი ტექნიკის გამოყენებით
რატომ უწოდებენ ტრიგონომეტრიულ ფუნქციებს წრიულ ფუნქციებს?

ტრიგონომეტრიულ ფუნქციებს ზოგჯერ წრიულ ფუნქციებსაც უწოდებენ. ეს იმიტომ ხდება, რომ ორი ფუნდამენტური ტრიგონომეტრიული ფუნქცია - სინუსი და კოსინუსი - განისაზღვრება, როგორც P წერტილის კოორდინატები, რომელიც მოძრაობს რადიუსის 1-ის ერთეული წრის გარშემო. სინუსი და კოსინუსი იმეორებენ თავიანთ გამოსავალს რეგულარული ინტერვალებით
როგორ ამრავლებთ რაციონალურ ფუნქციებს?

Q და S არ უდრის 0-ს. ნაბიჯი 1: შეადარეთ როგორც მრიცხველი, ასევე მნიშვნელი. ნაბიჯი 2: ჩაწერეთ როგორც ერთი წილადი. ნაბიჯი 3: რაციონალური გამოხატვის გამარტივება. ნაბიჯი 4: გაამრავლეთ დარჩენილი ფაქტორები მრიცხველში და/ან მნიშვნელში. ნაბიჯი 1: შეაფასეთ როგორც მრიცხველი, ასევე მნიშვნელი. ნაბიჯი 2: ჩაწერეთ როგორც ერთი წილადი
