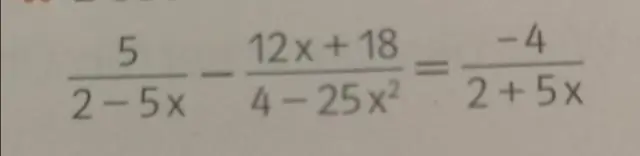
- ავტორი Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:37.
- ბოლოს შეცვლილი 2025-01-22 17:03.
THE კუთხეების მეთოდი გამოსადეგი ნაკრები (რეგიონი), S. Იპოვო ყველა წვეროს ზუსტი კოორდინატი ( კუთხე პუნქტები) S. შეაფასეთ ობიექტური ფუნქცია, P, თითოეულ წვეროზე მაქსიმალური (თუ ის არსებობს) არის P-ის უდიდესი მნიშვნელობა წვეროზე. მინიმალური არის P-ის უმცირესი მნიშვნელობა წვეროზე.
შემდგომში შეიძლება ისიც იკითხოს, როგორია LPP-ის გადაჭრის მეთოდები?
ხაზოვანი პროგრამირების ამოცანების ამოხსნის გრაფიკული მეთოდი
- შემოთავაზებული ვიდეოები.
- ნაბიჯი 1: ჩამოაყალიბეთ LP (ხაზოვანი პროგრამირება) პრობლემა.
- ნაბიჯი 2: შექმენით გრაფიკი და დახაზეთ შეზღუდვის ხაზები.
- ნაბიჯი 3: განსაზღვრეთ თითოეული შეზღუდვის ხაზის სწორი მხარე.
- ნაბიჯი 4: იდენტიფიცირება შესაძლებელი გადაწყვეტის რეგიონი.
- ნაბიჯი 5: დახაზეთ ობიექტური ფუნქცია გრაფიკზე.
- ნაბიჯი 6: იპოვნეთ ოპტიმალური წერტილი.
რა არის ალგებრული მეთოდი ხაზოვან პროგრამირებაში? Ალგებრა და Simplex მეთოდი . ა ხაზოვანი პროგრამირების პრობლემა (LP) არის ოპტიმიზაციის პრობლემა სადაც ყველა ცვლადი უწყვეტია, მიზანი არის a ხაზოვანი (გადაწყვეტილების ცვლადებთან მიმართებაში) ფუნქცია, და შესაძლებელი რეგიონი განისაზღვრება სასრული რაოდენობით ხაზოვანი უტოლობები ან განტოლებები.
აქ, როგორ გამოვთვალოთ კუთხის წერტილები წრფივი პროგრამირებაში?
The კუთხის წერტილები არის შესაძლებელი რეგიონის წვეროები. როდესაც თქვენ გაქვთ სისტემის გრაფიკი ხაზოვანი უტოლობები, მაშინ შეგიძლიათ შეხედოთ გრაფიკს და მარტივად თქვათ სად არის კუთხის წერტილები არიან. შეიძლება დაგჭირდეთ სისტემის გადაჭრა ხაზოვანი განტოლებები იპოვე ზოგიერთი კოორდინატი ქულები შუაში.
რა არის კუთხის წერტილის ამოხსნის მეთოდი?
The კუთხის წერტილის გადაწყვეტის მეთოდი შედგება ოთხი ძირითადი ნაბიჯისგან:: განსაზღვრეთ თითოეული წვერის კოორდინატები ( კუთხის წერტილი ) შესაძლებელი რეგიონის.: გამოთვალეთ ობიექტური ფუნქციის მნიშვნელობა თითოეულზე კუთხის წერტილი .: დაადგინეთ ობიექტური ფუნქცია მაქსიმალური მნიშვნელობით.
გირჩევთ:
როგორ გადაჭრით პროპორციის პრობლემას?

პირველ რიგში, დაწერეთ პროპორცია, გამოტოვებული ტერმინისთვის ასოს გამოყენებით. ჩვენ ვპოულობთ ჯვარედინი ნამრავლებს 20-ჯერ x-ზე და 50-ჯერ 30-ზე გამრავლებით. შემდეგ გავყოთ და ვიპოვოთ x. ყურადღებით შეისწავლეთ ეს ნაბიჯი, რადგან ეს არის ტექნიკა, რომელსაც ხშირად გამოვიყენებთ ალგებრაში
როგორ არის მსგავსი წრფივი უტოლობებისა და წრფივი განტოლებების ამოხსნა?

წრფივი უტოლობების ამოხსნა ძალიან ჰგავს წრფივი განტოლებების ამოხსნას. მთავარი განსხვავება ისაა, რომ თქვენ აბრუნებთ უტოლობის ნიშანს უარყოფით რიცხვზე გაყოფისას ან გამრავლებისას. წრფივი უტოლობების გრაფიკას კიდევ რამდენიმე განსხვავება აქვს. ნაწილი, რომელიც დაჩრდილულია, მოიცავს მნიშვნელობებს, სადაც წრფივი უტოლობა არის ჭეშმარიტი
როგორ გადაჭრით ფერდობის პრობლემას?

ფერდობის ამოცნობა, მ. ეს შეიძლება გაკეთდეს დახრილობის გამოთვლით ხაზის ორ ცნობილ წერტილს შორის დახრილობის ფორმულის გამოყენებით. იპოვეთ y-კვეთა. ეს შეიძლება გაკეთდეს დახრილობის და წერტილის (x, y) წრფის ჩანაცვლებით დახრილობა-კვეთის ფორმულით და შემდეგ ამოხსნით b-ს
როგორ ამოხსნით წრფივ განტოლებებს გრაფიკული მეთოდით?

გრაფიკული გადაწყვეტა შეიძლება გაკეთდეს ხელით (გრაფიკულ ქაღალდზე), ან გრაფიკული კალკულატორის გამოყენებით. წრფივი განტოლებათა სისტემის გრაფიკის დახატვა ისეთივე მარტივია, როგორც ორი სწორი ხაზის გრაფიკის დახატვა. როდესაც ხაზები გრაფიკულად არის დახატული, გამოსავალი იქნება (x,y) მოწესრიგებული წყვილი, სადაც ორი წრფე იკვეთება (ჯვარედინი)
რა არის წრფივი პროგრამირების მარტივი მეთოდი?
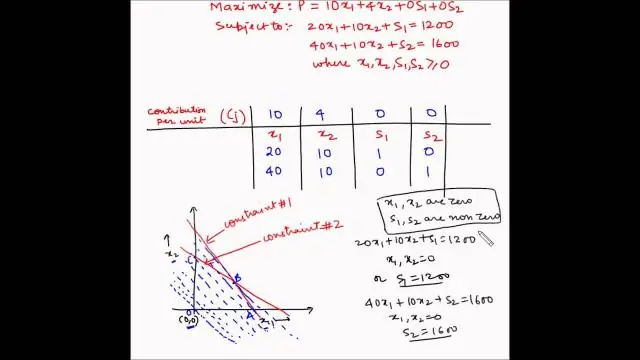
მარტივი მეთოდი. მარტივი მეთოდი, სტანდარტული ტექნიკა წრფივ პროგრამირებაში ოპტიმიზაციის პრობლემის გადასაჭრელად, რომელიც ჩვეულებრივ მოიცავს ფუნქციას და უტოლობად გამოხატულ რამდენიმე შეზღუდვას. უტოლობები განსაზღვრავენ მრავალკუთხედს (იხ. მრავალკუთხედი) და ამონახსნი ჩვეულებრივ ერთ-ერთ წვეროზეა
