- ავტორი Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:37.
- ბოლოს შეცვლილი 2025-01-22 17:03.
პასუხი: სკალირება არის რიცხვის ზომის შეცვლის პროცესი მიერ ა წილადი ეს არის 1-ზე მეტი ან ნაკლები.
ასევე, რა არის გამრავლება, როგორც მასშტაბირება?
ინტერპრეტაცია გამრავლება, როგორც მასშტაბირება (ზომის შეცვლა), მიერ: პროდუქტის ზომის შედარება ერთი ფაქტორის ზომასთან მეორე ფაქტორის ზომის საფუძველზე, მითითებულის შესრულების გარეშე გამრავლება ; და ახსნა რატომ მრავლდება მოცემული რიცხვი 1-ზე მეტი წილადით იწვევს პროდუქტს უფრო დიდზე
გარდა ამისა, როგორ მასშტაბებს? ნაბიჯები
- გაზომეთ ობიექტი, რომლის მასშტაბირებასაც აპირებთ.
- შეარჩიეთ თანაფარდობა თქვენი მასშტაბური ნახატისთვის.
- გადაიყვანეთ რეალური გაზომვები თანაფარდობით.
- დაიწყეთ პერიმეტრის დახაზვა სწორი სეგმენტით, როდესაც ეს შესაძლებელია.
- ხშირად მიმართეთ ორიგინალურ ნახატს.
- გამოიყენეთ ძაფის ნაჭერი არარეგულარული სურათების მასშტაბური სიგრძის შესამოწმებლად.
ასევე იცოდე, რატომ მცირდება წილადები გამრავლებისას?
გამრავლება მიერ „სათანადო წილადი ” აკეთებს რიცხვს უფრო პატარა რადგან ის გაყოფის ტოლფასია და გაყოფა უფრო დიდ რიცხვს ქმნის უფრო პატარა . თუმცა, ის ქმნის რიცხვს უფრო პატარა მხოლოდ იმ შემთხვევაში, თუ მრიცხველი<მნიშვნელი; წინააღმდეგ შემთხვევაში, ეს ადიდებს რიცხვს, რომელიც იხილეთ ქვემოთ.
რა არის მასშტაბირება მარტივი წილადებით?
ახსენი ეს, რომ აღწერო რამხელა იყო რაღაც მასშტაბური ქვემოთ, ჩვენ ხშირად ვიყენებთ თანაფარდობას ან მარტივი წილადები . ისინი თავად წყვეტენ თანაფარდობას სკალირება ქვემოთ, მაგალითად, 1:2 (ზომის ნახევარი) ან 1:3 (ზომის ერთი მესამედი). დააფიქსირე რომ სკალირება ქვემოთ იგივეა, რაც გამრავლება 1-ზე ნაკლები მნიშვნელობით.
გირჩევთ:
როგორია ნატანის ზომის სწორი თანმიმდევრობა?

როგორია ნატანის ზომის სწორი თანმიმდევრობა უმცირესიდან დიდამდე? ა. თიხა, სილა, ქვიშა, გრანულა, კენჭი, რიყის, ლოდი. ნაცრისფერი ნალექები შეიცავს რკინას, ხოლო ის, ვინც ყავისფერ შოკოლადისფერამდეა, მაღალი სილიციუმის შემცველობით
როგორია ჯგუფში ატომის ზომის პერიოდული ტენდენცია ზემოდან ქვემოდან?
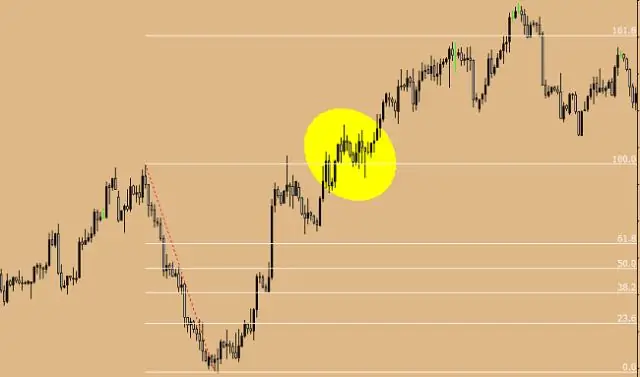
ჯგუფის ზემოდან ქვევით ქვევით, ელექტრონეგატიურობა მცირდება. ეს იმიტომ ხდება, რომ ატომური რიცხვი იზრდება ჯგუფში და, შესაბამისად, იზრდება მანძილი ვალენტურ ელექტრონებსა და ბირთვს შორის, ან უფრო დიდი ატომური რადიუსი
რა ნაბიჯებია რაციონალური ალგებრული გამონათქვამის გამრავლებისას?
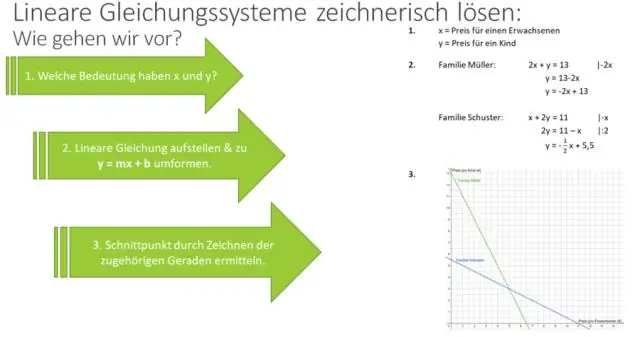
Q და S არ უდრის 0-ს. ნაბიჯი 1: შეადარეთ როგორც მრიცხველი, ასევე მნიშვნელი. ნაბიჯი 2: ჩაწერეთ როგორც ერთი წილადი. ნაბიჯი 3: რაციონალური გამოხატვის გამარტივება. ნაბიჯი 4: გაამრავლეთ დარჩენილი ფაქტორები მრიცხველში და/ან მნიშვნელში. ნაბიჯი 1: შეაფასეთ როგორც მრიცხველი, ასევე მნიშვნელი. ნაბიჯი 2: ჩაწერეთ როგორც ერთი წილადი
რომელი ტრანსფორმაცია შეცვლის სურათს A ფიგურად B?
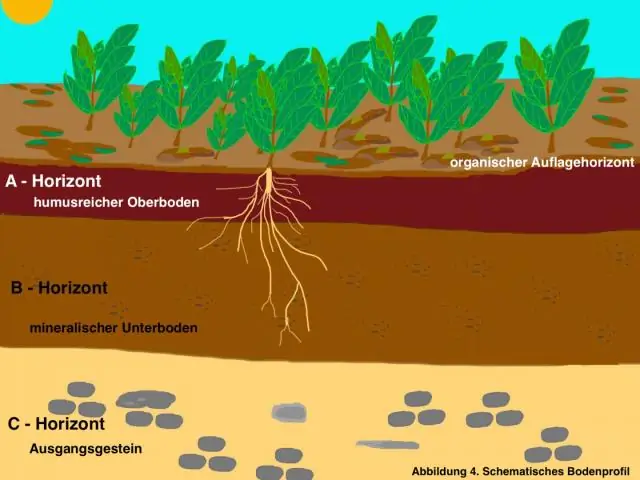
ნათქვამია, რომ ორი ფიგურა თანმიმდევრულია, თუ ერთის მიღება შესაძლებელია მეორისგან თარგმანის, ასახვისა და ბრუნვის თანმიმდევრობით. თანმიმდევრულ ფიგურებს აქვთ იგივე ზომა და ფორმა. A ფიგურის B ფიგურად გადაქცევისთვის, თქვენ უნდა აისახოთ იგი y ღერძზე და გადათარგმნოთ ერთი ერთეული მარცხნივ
რა არის სპონტანური პროცესი და არასპონტანური პროცესი?

სპონტანური პროცესი არის ის, რომელიც ხდება გარე ჩარევის გარეშე. არასპონტანური პროცესი არ მოხდებოდა გარე ჩარევის გარეშე
