Სარჩევი:
ვიდეო: როგორ იპოვით ცენტრალურ კუთხეს სექტორის ფართობისა და რადიუსის გათვალისწინებით?
2024 ავტორი: Miles Stephen | [email protected]. ბოლოს შეცვლილი: 2024-01-18 08:16
ცენტრალური კუთხის განსაზღვრა სექტორის ზონიდან
- (პრ2) × ( ცენტრალური კუთხე გრადუსებში ÷ 360 გრადუსი) = სექტორის ტერიტორია . თუ ცენტრალური კუთხე იზომება რადიანებში, ამის ნაცვლად ფორმულა ხდება:
- სექტორის ტერიტორია = r2 × ( ცენტრალური კუთხე რადიანებში ÷ 2).
- (θ ÷ 360 გრადუსი) × πr2.
- (52.3 ÷ 100π) × 360.
- (52.3 ÷ 314) × 360.
ამ გზით, როგორ იპოვით რადიუსზე მოცემულ ცენტრალურ კუთხეს?
იპოვე The ცენტრალური კუთხე რკალის სიგრძიდან და რადიუსი თქვენ ასევე შეგიძლიათ გამოიყენოთ რადიუსი წრის და რკალის სიგრძის მდე იპოვე The ცენტრალური კუთხე . დარეკეთ საზომი ცენტრალური კუთხე თ. მაშინ: θ = s ÷ r, სადაც s არის რკალის სიგრძე და r არის რადიუსი.
გარდა ზემოთ, როგორ იპოვით სექტორის ცენტრალურ კუთხეს? ცენტრალური კუთხის განსაზღვრა Დან სექტორი ფართობი სხვა სიტყვებით რომ ვთქვათ: (πr2) × ( ცენტრალური კუთხე გრადუსებში ÷ 360 გრადუსი) = სექტორი ფართობი. თუ ცენტრალური კუთხე იზომება რადიანებში, ფორმულა ნაცვლად ხდება: სექტორი ფართობი = r2 × ( ცენტრალური კუთხე რადიანებში ÷ 2).
გარდა ზემოთ, რა არის სექტორის ფართობი?
The სექტორის ფართობი L-ის მიხედვით შეიძლება მივიღოთ ჯამის გამრავლებით ფართობი πr2 L-ის შეფარდებით მთლიან პერიმეტრზე 2πr.
რა არის გარშემოწერილობის ფორმულა?
ა-ს გარშემოწერილობის გამოსათვლელად წრე გამოიყენეთ ფორმულა C = πd, სადაც "C" არის გარშემოწერილობა, "d" არის დიამეტრი და π არის 3.14. თუ დიამეტრის ნაცვლად რადიუსი გაქვთ, დიამეტრის მისაღებად გაამრავლეთ ის 2-ზე. ასევე შეგიძლიათ გამოიყენოთ a-ს გარშემოწერილობის ფორმულა წრე რადიუსის გამოყენებით, რომელიც არის C = 2πr.
გირჩევთ:
როგორ იპოვით ვექტორის კომპონენტურ ფორმას სიდიდისა და კუთხის გათვალისწინებით?
ვიდეო ამის გათვალისწინებით, არის 0 ერთეული ვექტორი? ა ერთეული ვექტორი არის ვექტორი რომელსაც აქვს სიდიდე 1. აღნიშვნა წარმოადგენს ნორმას ან სიდიდეს ვექტორი v ძირითადი ერთეული ვექტორები მე = (1, 0 ) და j = ( 0 , 1) რომელთა სიგრძეა 1 და აქვთ მიმართულებები დადებითი x ღერძის და y ღერძის გასწვრივ შესაბამისად.
როგორ ვიპოვოთ წრის სექტორის სიგრძე?
ცენტრალური კუთხის, რომელიც დაქვეითებულია ძირითადი რკალით, ზომა აღემატება 180°-ს. რკალის სიგრძის ფორმულა გამოიყენება წრის რკალის სიგრძის საპოვნელად; l=rθ l = r θ, სადაც θ არის რადიანებში. ნაპოვნია სექტორის ფართობი A=12θr2 A = 1 2 θ r 2, სადაც θ არის რადიანებში
როგორ მოვძებნოთ რკალის სიგრძე და სექტორის ფართობი?
ცენტრალური კუთხის, რომელიც დაქვეითებულია ძირითადი რკალით, ზომა აღემატება 180°-ს. რკალის სიგრძის ფორმულა გამოიყენება წრის რკალის სიგრძის საპოვნელად; l=rθ l = r θ, სადაც θ არის რადიანებში. ნაპოვნია სექტორის ფართობი A=12θr2 A = 1 2 θ r 2, სადაც θ არის რადიანებში
როგორ იპოვით ზომებს ფართობისა და პერიმეტრის მიცემისას?
სიგრძისა და სიგანის პოვნა, როდესაც გეცოდინებათ ფართობი და პერიმეტრი, თუ თქვენ იცით მანძილი მართკუთხედის ირგვლივ, რომელიც არის მისი პერიმეტრი, შეგიძლიათ ამოხსნათ წყვილი განტოლება L და W. პირველი განტოლება არის ფართობი, A = L ⋅ W, და მეორე არის ის, რომ პერიმეტრზე, P = 2L + 2W
როგორ მოვძებნოთ სექტორის კუთხე წრიულ დიაგრამაში?
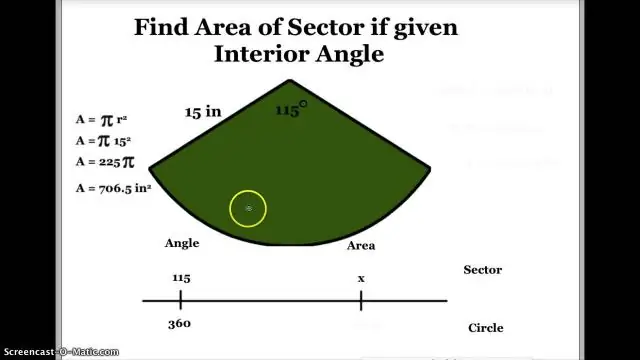
1 პასუხი ნებისმიერ სექტორში გასათვალისწინებელია 3 ნაწილი: რკალის სიგრძე არის წრეწირის წილადი.ესექტორის ფართობი არის მთელი ფართობის წილადი. ეს კუთხური კუთხე არის 360°-ის წილადი, თუ სექტორი არის წრიული დიაგრამის 20%, მაშინ ამ ნაწილების თითოეული არის მთლიანის 20%. 20%×360° 20100×360=72°