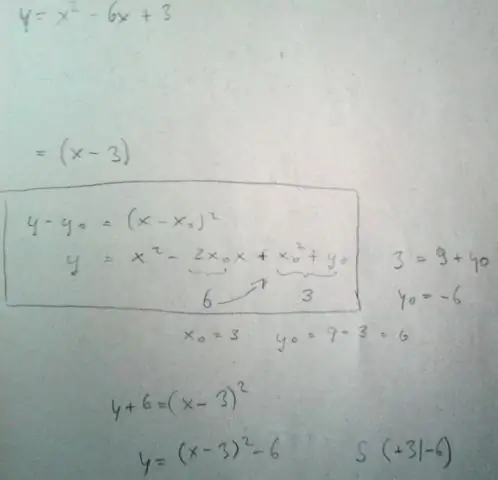
- ავტორი Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:37.
- ბოლოს შეცვლილი 2025-06-01 05:04.
ა კვადრატული ფუნქცია არის f(x) = ცულის ერთ-ერთი ფორმა2 + bx + c, სადაც a, b და c არის რიცხვები, რომელთა ტოლი არ არის ნულის. გრაფიკი ა კვადრატული ფუნქცია არის მრუდი, რომელსაც პარაბოლა ჰქვია. პარაბოლები შეიძლება გაიხსნას ზევით ან ქვევით და განსხვავდებოდეს "სიგანით" ან "ციცაბოთი", მაგრამ მათ ყველას აქვთ იგივე ძირითადი "U" ფორმა.
აქედან გამომდინარე, რა არის A წვერო ფორმაში?
y = a(x - h)2 + k, სადაც (h, k) არის წვერო . "ა"-ში წვერო ფორმა არის იგივე "ა", რაც. y-ში = ცული2 + bx + c (ანუ ორივე a-ს აქვს ზუსტად იგივე მნიშვნელობა). ნიშანი "a"-ზე გიჩვენებთ, იხსნება თუ ქვევით კვადრატი.
როგორ განვსაზღვროთ, რომ განტოლება ფუნქციაა? შედარებით ადვილია დადგინდეს თუ არა ა განტოლება არის ფუნქცია y-ის ამოხსნით. როცა გაძლევენ განტოლება და კონკრეტული მნიშვნელობა x-ისთვის, უნდა იყოს მხოლოდ ერთი შესაბამისი y-მნიშვნელობა ამ x-მნიშვნელობისთვის. მაგალითად, y = x + 1 არის a ფუნქცია რადგან y ყოველთვის იქნება x-ზე ერთით დიდი.
ამ გზით, როგორ წერთ პარაბოლას განტოლებას?
ამისთვის პარაბოლები რომ გახსნილია გვერდით, სტანდარტული ფორმა განტოლება არის (y - k)^2 = 4p(x - h). წვერო ან წვერი ჩვენი პარაბოლა მოცემულია წერტილით (h, k). ამისთვის პარაბოლები რომელიც იხსნება ზევით და ქვევით, ფოკუსის წერტილი მოცემულია (h, k + p). ამისთვის პარაბოლები რომელიც გვერდით იხსნება, ფოკუსის წერტილი არის (h + p, k).
რა არის კვადრატული ფუნქციის სტანდარტული ფორმა?
ა კვადრატული ფუნქცია არის ფუნქცია მეორე ხარისხის. გრაფიკი ა კვადრატული ფუნქცია არის პარაბოლა . გენერალი კვადრატული ფუნქციის ფორმა არის f(x)=ax2+bx+c სადაც a, b და c არის რეალური რიცხვები და a≠0. The კვადრატული ფუნქციის სტანდარტული ფორმა არის f(x)=a(x−h)2+k.
გირჩევთ:
როგორ ამოხსნათ კვადრატული განტოლება ნულოვანი ფაქტორის კანონის გამოყენებით?

აქედან შეგვიძლია დავასკვნათ, რომ: თუ რომელიმე ორი რიცხვის ნამრავლი არის ნული, მაშინ ერთი ან ორივე რიცხვი არის ნული. ანუ, თუ ab = 0, მაშინ a = 0 ან b = 0 (რაც მოიცავს შესაძლებლობას, რომ a = b = 0). ამას ეწოდება Null Factor Law; და ჩვენ მას ხშირად ვიყენებთ კვადრატული განტოლებების ამოსახსნელად
როგორ იპოვით კვადრატული ფუნქციის სიმბოლურ წარმოდგენას?

კვადრატული ფუნქციები სიმბოლურად შეიძლება წარმოდგენილი იყოს განტოლებით, y(x) = ax2 + bx + c, სადაც a, b და c არის მუდმივები და a ≠ 0. ეს ფორმა მოიხსენიება როგორც სტანდარტული ფორმა
როგორ დავწეროთ კვადრატული განტოლება C++-ში?
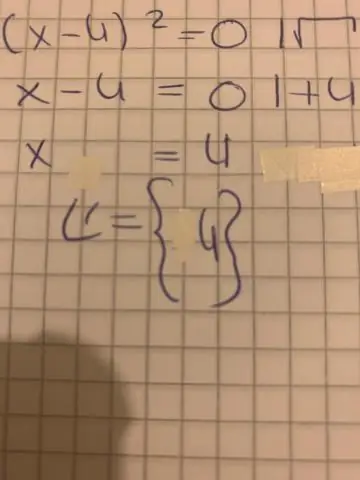
პროგრამა 2: იპოვეთ b და c კვადრატულ განტოლებაში #include #include int main(){float a,b,c; float d,root1,root2; printf('შეიყვანეთ კვადრატული განტოლება ფორმატში ax^2+bx+c: '); scanf('%fx^2%fx%f',&a,&b,&c); d = b * b - 4 * a * c;
როგორ გადაიყვანოთ კვადრატული განტოლება წვერო ფორმის კალკულატორში?

კალკულატორი ძირითადი ფორმიდან წვეროს ფორმაში გადასაყვანად y=x2+3x+5. x2+3x+5= || +(p2)2-(p2)2=0. || a2+2ab+b2=(a+b)2. || -1⋅-1=+1. xS=-32=-1,5. yS=-(32)2+5=2.75
როგორ მოვძებნოთ კვადრატული ფუნქციის მაქსიმალური მნიშვნელობა?

თუ თქვენ გეძლევათ ფორმულა y = ax2 + bx + c, მაშინ შეგიძლიათ იპოვოთ მაქსიმალური მნიშვნელობა ფორმულის გამოყენებით max =c- (b2 / 4a). თუ თქვენ გაქვთ განტოლება y = a(x-h)2 + k და ტერმინი უარყოფითია, მაშინ მაქსიმალური მნიშვნელობა არის k
