ვიდეო: როგორ იპოვით კვადრატული ფუნქციის სიმბოლურ წარმოდგენას?
2024 ავტორი: Miles Stephen | [email protected]. ბოლოს შეცვლილი: 2023-12-15 23:37
კვადრატული ფუნქციები შეიძლება სიმბოლურად იყოს წარმოდგენილი განტოლება , y(x) = ცული2 + bx + c, სადაც a, b და c არის მუდმივები, და a ≠ 0. ეს ფორმა მოიხსენიება როგორც სტანდარტული ფორმა.
ხალხი ასევე იკითხავს, რა არის ფუნქციის სიმბოლური წარმოდგენა?
ფუნქციები . თქვენ ალბათ ყველაზე კარგად იცნობთ სიმბოლური წარმოდგენა დან ფუნქციები , როგორიცაა განტოლება, y = f(x). ფუნქციები შეიძლება წარმოდგენილი იყოს ცხრილებით, სიმბოლოები , ან გრაფიკები.
ანალოგიურად, როგორ განვსაზღვროთ კვადრატული გრაფიკის ფორმა? პარაბოლას ფორმა
- თუ a>0, მაშინ პარაბოლას აქვს მინიმალური წერტილი და ის იხსნება ზემოთ (U- ფორმის) მაგ.
- თუ a<0, მაშინ პარაბოლას აქვს მაქსიმალური წერტილი და ის იხსნება ქვემოთ (n- ფორმის) მაგ.
- (ა) შეამოწმეთ a>0 თუ a<0, რათა გადაწყვიტოთ არის თუ არა ის U- ფორმის თუ n-ის.
- (გ) y-კვეთის კოორდინატები (ჩანაცვლება x=0).
შესაბამისად, როგორ წარმოადგენთ კვადრატულ ფუნქციას?
გრაფიკები. ა კვადრატული ფუნქცია არის f(x) = ცულის ერთ-ერთი ფორმა2 + bx + c, სადაც a, b და c არის რიცხვები, რომელთა ტოლი არ არის ნულის. გრაფიკი ა კვადრატული ფუნქცია არის მრუდი, რომელსაც პარაბოლა ჰქვია. პარაბოლები შეიძლება გაიხსნას ზევით ან ქვევით და განსხვავდებოდეს "სიგანით" ან "ციცაბოთი", მაგრამ მათ ყველას აქვთ იგივე ძირითადი "U" ფორმა.
როგორ ამოხსნით ფუნქციას?
ამისთვის ფუნქციები , ორი აღნიშვნა ზუსტად ერთსა და იმავეს ნიშნავს, მაგრამ "f (x)" გაძლევთ მეტ მოქნილობას და მეტ ინფორმაციას. თქვენ ამბობდით "y = 2x + 3; გადაჭრა y-სთვის, როდესაც x = –1". ახლა თქვენ თქვით "f (x) = 2x + 3; იპოვეთ f (–1)" (გამოითქმის როგორც "f-of-x უდრის 2x-ს პლუს სამი; იპოვეთ f-of-უარყოფითი-ერთი").
გირჩევთ:
რა არის კვადრატული ფუნქციის განტოლება?
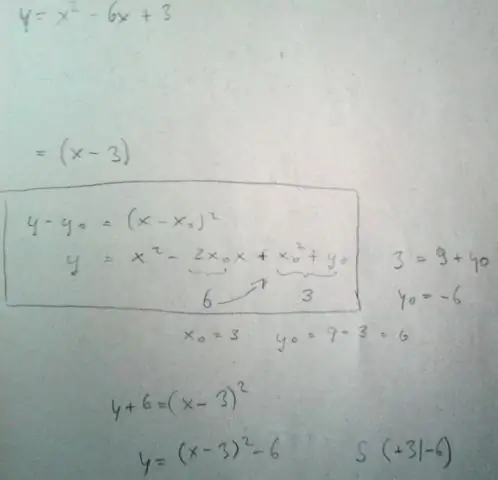
კვადრატული ფუნქცია არის ერთ-ერთი ფორმა f(x) = ax2 + bx + c, სადაც a, b და c არის რიცხვები, რომელთა ტოლი არ არის ნული. კვადრატული ფუნქციის გრაფიკი არის მრუდი, რომელსაც პარაბოლა ეწოდება. პარაბოლები შეიძლება გაიხსნას ზევით ან ქვევით და განსხვავდებოდეს "სიგანით" ან "ციცაბოში", მაგრამ მათ ყველას აქვთ იგივე ძირითადი "U" ფორმა
როგორ მოვძებნოთ ტრიგ ფუნქციის მეორე წარმოებული?
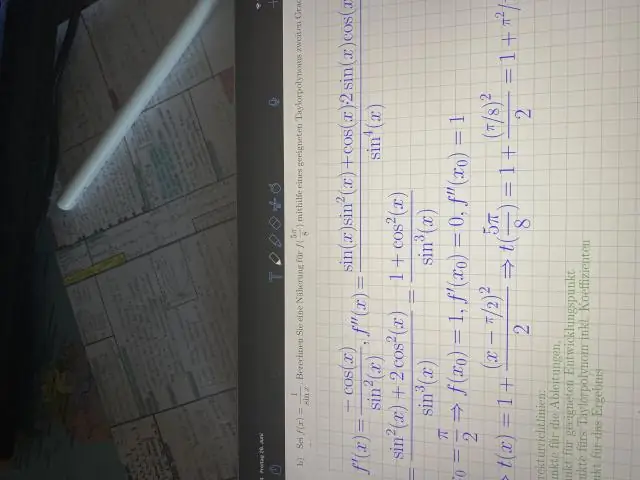
ვიდეო ასე რომ, რა არის 6 ტრიგ ფუნქციის წარმოებულები? ტრიგონომეტრიული ფუნქციების წარმოებულები. ძირითადი ტრიგონომეტრიული ფუნქციები მოიცავს შემდეგ 6 ფუნქციას: სინუსი ( ცოდვა x), კოსინუსი ( cos x), ტანგენსი (tanx), კოტანგენსი (cotx), სეკანტი (secx) და კოსეკანტი (cscx).
როგორ დავწეროთ ფუნქციის წესი შეყვანის გამომავალი ცხრილისთვის?
ცხრილის რიცხვების თითოეული წყვილი დაკავშირებულია იგივე ფუნქციის წესით. ეს წესია: გაამრავლეთ თითოეული შეყვანილი რიცხვი (egin{align*}xend{align*}-value) 3-ზე, რათა იპოვოთ გამომავალი ნომერი (egin{align*}yend{align*}-მნიშვნელობა). თქვენ შეგიძლიათ გამოიყენოთ მსგავსი წესი ამ ფუნქციის სხვა მნიშვნელობების მოსაძებნად
როგორ იპოვით სამუშაო ფუნქციის ზღურბლის სიხშირეს?
ამის გამოსათვლელად დაგჭირდებათ მასალაზე სინათლის ინციდენტის ენერგია და გამოდევნილი ფოტოელექტრონის კინეტიკური ენერგია. E = hf-ის გამოყენებით ჩვენ შეგვიძლია გამოვთვალოთ სინათლის სიხშირე ენერგიაში ჩასვლისა და f-ის გამოანგარიშებით. ეს იქნება ბარიერის სიხშირე
როგორ მოვძებნოთ კვადრატული ფუნქციის მაქსიმალური მნიშვნელობა?
თუ თქვენ გეძლევათ ფორმულა y = ax2 + bx + c, მაშინ შეგიძლიათ იპოვოთ მაქსიმალური მნიშვნელობა ფორმულის გამოყენებით max =c- (b2 / 4a). თუ თქვენ გაქვთ განტოლება y = a(x-h)2 + k და ტერმინი უარყოფითია, მაშინ მაქსიმალური მნიშვნელობა არის k