Სარჩევი:
ვიდეო: რამდენი რადიალური კვანძია 4s ორბიტალში?
2024 ავტორი: Miles Stephen | [email protected]. ბოლოს შეცვლილი: 2023-12-15 23:37
რაოდენობა კვანძები დაკავშირებულია ძირითად კვანტურ რიცხვთან, n. ნ.ს ორბიტალური აქვს (n-1) რადიალური კვანძები , ასე რომ 4წ - ორბიტალური აქვს (4-1) = 3 კვანძები , როგორც ნაჩვენებია ზემოთ ნაკვეთზე.
შემდგომში შეიძლება ასევე იკითხოს, რამდენი რადიალური კვანძია 4s ორბიტალში?
3
შეიძლება ასევე იკითხოს, რამდენი კვანძია ორბიტალში? საერთო რაოდენობა კვანძები ამაში იმყოფება ორბიტალური უდრის n-1-ს. ამ შემთხვევაში 3-1=2 არის 2 სულ კვანძები . კვანტური რიცხვი ℓ განსაზღვრავს კუთხის რაოდენობას კვანძები ; არის 1 კუთხოვანი კვანძი , კონკრეტულად xy სიბრტყეზე, რადგან ეს არის pზ ორბიტალური.
ანალოგიურად, რამდენი კვანძი შეიძლება ჰქონდეს 4s ორბიტალს?
სამი კვანძი
როგორ მოვძებნოთ რადიალური კვანძების რაოდენობა ორბიტალში?
არსებობს ორი სახის კვანძი: რადიალური და კუთხოვანი
- კუთხოვანი კვანძების რაოდენობა ყოველთვის უდრის ორბიტალური კუთხური იმპულსის კვანტურ რიცხვს, l.
- რადიალური კვანძების რაოდენობა = კვანძების საერთო რაოდენობა გამოკლებული კუთხოვანი კვანძების რაოდენობა = (n-1) - l.
გირჩევთ:
რამდენი EcoRI ადგილია ლამბდა დნმ-ში?
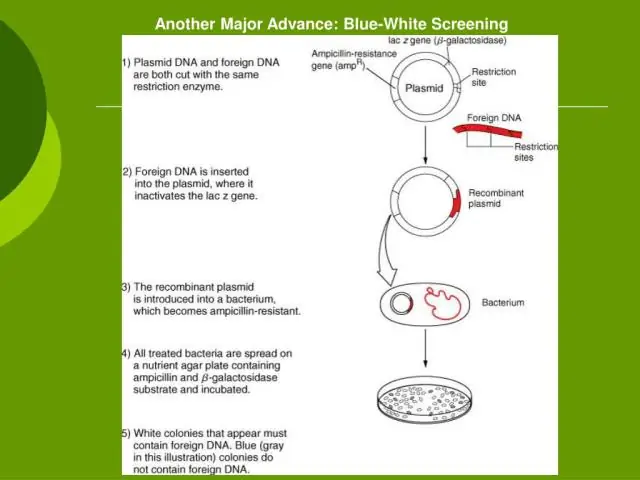
ამ ექსპერიმენტში გამოყენებული ლამბდას დნმ იზოლირებულია როგორც წრფივი მოლეკულა E. coli ბაქტერიოფაგის ლამბდასგან. იგი შეიცავს დაახლოებით 49000 ბაზის წყვილს და აქვს 5 ამოცნობის ადგილი Eco RI-სთვის და 7 Hind III-ისთვის
რა არის რადიალური ალბათობის განაწილების მრუდი?
რადიალური განაწილების მრუდი იძლევა წარმოდგენას ელექტრონის სიმკვრივის შესახებ ბირთვიდან რადიალურ მანძილზე. 4πr2ψ2-ის მნიშვნელობა (რადიალური ალბათობის სიმკვრივის ფუნქცია) ხდება ნულოვანი კვანძის წერტილში, რომელიც ასევე ცნობილია როგორც რადიალური კვანძი. სადაც n = ძირითადი კვანტური რიცხვი და l = აზიმუთალური კვანტური რიცხვი
რამდენი კვანძია ანტიბონგული ორბიტალში?
თითოეული ორბიტალი შეიცავს ორ ელექტრონს. π4 დაπ5 არის დეგენერაციული ანტიბმატური ორბიტალები, რომელთა ორი კვანძი მართი კუთხით არის ერთმანეთთან. π6 არის ანტიბონგული ორბიტალი სამი კვანძით
რადიალური სიმეტრია ასიმეტრიულია?
ცხოველთა მხოლოდ რამდენიმე ჯგუფი ავლენს რადიალურ სიმეტრიას, ხოლო ასიმეტრია არის phyla Porifera (სპონგების) უნიკალური თვისება
რა არის რადიალური ალბათობის სიმკვრივის ფუნქცია?
რადიალური განაწილების ფუნქცია იძლევა ალბათობის სიმკვრივეს, რომ ელექტრონი აღმოჩნდეს სფეროს ზედაპირზე ნებისმიერ ადგილას, რომელიც მდებარეობს პროტონიდან r მანძილზე. ვინაიდან სფერული ზედაპირის ფართობი არის 4πr2, რადიალური განაწილების ფუნქცია მოცემულია (4 pi r^2 R(r) ^* R(r)]