Სარჩევი:
ვიდეო: როგორ ვიპოვოთ სამკუთხედის შუა სეგმენტის თეორემა?
2024 ავტორი: Miles Stephen | [email protected]. ბოლოს შეცვლილი: 2023-12-15 23:37
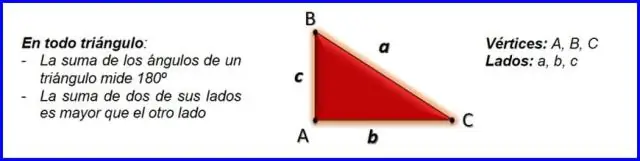
სამკუთხედის შუა სეგმენტის თეორემა ამბობს, რომ წრფის სეგმენტი, რომელიც აკავშირებს სამკუთხედის ნებისმიერი ორი გვერდის შუა წერტილებს, დააკმაყოფილებს შემდეგ თვისებებს:
- ხაზის სეგმენტი იქნება მესამე მხარის პარალელურად.
- ხაზის სეგმენტის სიგრძე იქნება მესამე მხარის სიგრძის ნახევარი.
ამის გარდა, რა არის შუა სეგმენტის თეორემა?
The შუა სეგმენტის თეორემა აღნიშნავს, რომ სეგმენტი, რომელიც აკავშირებს ორი მხარის შუა წერტილებს სამკუთხედის არის მესამე მხარის პარალელურად და ნახევრად სიგრძეზე.
გარდა ზემოთ, როგორ ვიპოვო სამკუთხედის სიგრძე? პითაგორას თეორემა (პითაგორას თეორემა) ჰიპოტენუზა არის მარჯვენა მხარის ყველაზე გრძელი მხარე. სამკუთხედი , და მდებარეობს სწორი კუთხის საპირისპიროდ. ასე რომ, თუ იცით სიგრძეები ორი მხარის, ყველაფერი რაც თქვენ უნდა გააკეთოთ არის ორი მხარის კვადრატი სიგრძეები , დაამატეთ შედეგი, შემდეგ აიღეთ ჯამის კვადრატული ფესვი, რომ მიიღოთ სიგრძე ჰიპოტენუზის.
ასევე იცოდეთ, როგორ გადაჭრით შუა სეგმენტს?
ხაზი DE არის ABC სამკუთხედის შუა სეგმენტი
- ის აკავშირებს სამკუთხედის ორი გვერდის ორ შუა წერტილს.
- იგი უდრის ბაზის სიგრძის ნახევარს.
- ის ბაზის პარალელურია.
- იგი ქმნის პატარა სამკუთხედს კუთხის იგივე ზომებით, პერიმეტრის ნახევარი და თავდაპირველი სამკუთხედის ფართობის მეოთხედი.
როგორ ვიპოვოთ სამკუთხედის პერიმეტრი?
მოძიება პერიმეტრი როდესაც ცნობილია სამი მხარის სიგრძე. დაიმახსოვრე ფორმულა პოვნისთვის პერიმეტრი ა სამკუთხედი . Თვის სამკუთხედი a, b და c გვერდებით, the პერიმეტრი P განისაზღვრება, როგორც: P = a + b + c.
გირჩევთ:
რა არის ტრაპეციის შუა სეგმენტის თეორემა?
ტრაპეციის შუა სეგმენტის თეორემა. სამკუთხედის შუა სეგმენტის თეორემა ამბობს, რომ სამკუთხედის ორი გვერდის შუა წერტილების დამაკავშირებელი ხაზი, რომელსაც შუა სეგმენტი ეწოდება, არის მესამე მხარის პარალელურად და მისი სიგრძე უდრის მესამე მხარის სიგრძის ნახევარს
როგორ ვიპოვოთ მართკუთხა სამკუთხედის დიაგონალი?
მართკუთხა სამკუთხედის დიაგონალის (ორჰიპოტენუზის) სიგრძის საპოვნელად, ჩაანაცვლეთ ორი პერპენდიკულარული გვერდის სიგრძე ფორმულით a2 +b2 = c2, სადაც a და b არის პერპენდიკულარული გვერდების სიგრძე და c არის ჰიპოტენუზის სიგრძე
რატომ არის, რომ ბლაგვი სამკუთხედის ორთოცენტრი უნდა იყოს სამკუთხედის გარე მხარეს?
გამოდის, რომ სამივე სიმაღლე ყოველთვის ერთსა და იმავე წერტილზე იკვეთება - სამკუთხედის ე.წ. ორთოცენტრი ყოველთვის არ არის სამკუთხედის შიგნით. თუ სამკუთხედი ბლაგვია, ის გარეთ იქნება. იმისათვის, რომ ეს მოხდეს, სიმაღლის ხაზები უნდა გაგრძელდეს ისე, რომ ისინი გადაკვეთონ
როგორ ვიპოვოთ სამკუთხედის მოპირდაპირე მხარე პითაგორას გამოყენებით?
მართკუთხა სამკუთხედები და პითაგორას თეორემა პითაგორას თეორემა, a2+b2=c2, a 2 + b 2 = c 2, შეიძლება გამოყენებულ იქნას მართკუთხა სამკუთხედის ნებისმიერი გვერდის სიგრძის საპოვნელად. მართი კუთხის მოპირდაპირე მხარეს ჰიპოტენუზა ეწოდება (გვერდი c ფიგურაში)
როგორ ვიპოვოთ წრფის სეგმენტის პერპენდიკულარული ბისექტრის განტოლება?
ჩაწერეთ განტოლება წერტილის დახრილობის სახით, y - k =m(x - h), რადგან ცნობილია პერპენდიკულარული ბისექტრის და (h, k) წერტილის დახრილობა, რომელსაც ბისექტრი გადის. ამოხსენით წერტილი-დახრის განტოლება y-სთვის, რომ მიიღოთ y = mx + b. გაანაწილეთ ფერდობის მნიშვნელობა. გადაიტანეთ k მნიშვნელობა განტოლების მარჯვენა მხარეს