
Სარჩევი:
- ავტორი Miles Stephen [email protected].
- Public 2023-12-15 23:37.
- ბოლოს შეცვლილი 2025-01-22 17:03.
არაწრფივი რეგრესია შეიძლება მოერგება სხვა მრავალი სახის მოსახვევებს, მაგრამ ის შეუძლია მოითხოვს მეტ ძალისხმევას, როგორც საუკეთესო მორგების პოვნაში, ასევე ინტერპრეტაცია დამოუკიდებელი ცვლადების როლი. გარდა ამისა, R-კვადრატი არ მოქმედებს არაწრფივი რეგრესია და ეს შეუძლებელია გამოთვალეთ p-მნიშვნელობები პარამეტრების შეფასებისთვის.
ამ გზით, შეიძლება თუ არა რეგრესია იყოს არაწრფივი?
სტატისტიკაში, არაწრფივი რეგრესია არის ფორმა რეგრესია ანალიზი, რომელშიც დაკვირვების მონაცემები მოდელირებულია ფუნქციით, რომელიც არის a არაწრფივი მოდელის პარამეტრების კომბინაცია და დამოკიდებულია ერთ ან მეტ დამოუკიდებელ ცვლადზე. მონაცემები დაყენებულია თანმიმდევრული მიახლოების მეთოდით.
შეიძლება ასევე ვიკითხოთ, არის თუ არა r კვადრატი მხოლოდ წრფივი რეგრესისთვის? ზოგადი მათემატიკური ჩარჩო ამისთვის რ - კვადრატში არ გამოდის სწორად, თუ რეგრესიის მოდელი არ არის ხაზოვანი . მიუხედავად ამ პრობლემისა, სტატისტიკური პროგრამული უზრუნველყოფის უმეტესობა მაინც ითვლის რ - კვადრატში არაწრფივი მოდელებისთვის. თუ იყენებთ რ - კვადრატში რომ აირჩიოთ საუკეთესო მოდელი , მიჰყავს სათანადო მხოლოდ მოდელი შემთხვევების 28-43%.
ამასთან დაკავშირებით, როგორ გამოვთვალოთ არაწრფივი რეგრესია?
თუ თქვენი მოდელი იყენებს განტოლება Y = a სახით0 + ბ1X1, ეს არის ხაზოვანი რეგრესია მოდელი. თუ არა, ეს არის არაწრფივი.
Y = f(X, β) + ε
- X = p პროგნოზირების ვექტორი,
- β = k პარამეტრების ვექტორი,
- f(-) = ცნობილი რეგრესიული ფუნქცია,
- ε = შეცდომის ტერმინი.
რა არის რეგრესიის ტიპები?
რეგრესიის სახეები
- ხაზოვანი რეგრესია. ეს არის რეგრესიის უმარტივესი ფორმა.
- პოლინომიური რეგრესია. ეს არის არაწრფივი განტოლების მორგების ტექნიკა დამოუკიდებელი ცვლადის პოლინომიური ფუნქციების აღებით.
- ლოგისტიკური რეგრესია.
- Quantile რეგრესია.
- ქედის რეგრესია.
- ლასოს რეგრესია.
- ელასტიური ბადის რეგრესია.
- ძირითადი კომპონენტების რეგრესია (PCR)
გირჩევთ:
რა არის ხაზოვანი რეგრესია R პროგრამირებაში?

წრფივი რეგრესია გამოიყენება უწყვეტი ცვლადის Y მნიშვნელობის პროგნოზირებისთვის ერთი ან მეტი შეყვანის პროგნოზირების ცვლადის საფუძველზე X. მიზანია დაადგინოს მათემატიკური ფორმულა პასუხის ცვლადს (Y) და პროგნოზირებულ ცვლადებს (Xs) შორის. თქვენ შეგიძლიათ გამოიყენოთ ეს ფორმულა Y-ის პროგნოზირებისთვის, როდესაც ცნობილია მხოლოდ X მნიშვნელობები
როგორ კეთდება სინუსოიდური რეგრესია კალკულატორზე?
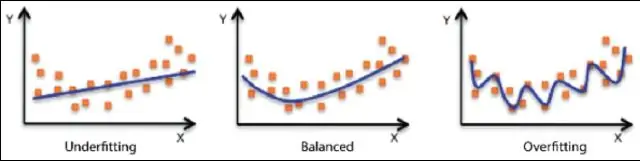
ვიდეო აქედან, როგორ გამოვთვალოთ სინუსოიდური რეგრესია? სინუსოიდური რეგრესია . დაარეგულირეთ A, B, C და D მნიშვნელობები ში განტოლება y = A*sin(B(x-C))+D რათა გააკეთოს a სინუსოიდური მრუდი შეესაბამება შემთხვევით გენერირებული მონაცემების მოცემულ კომპლექტს.
როგორ გამოვთვალოთ არაწრფივი რეგრესია?

თუ თქვენი მოდელი იყენებს განტოლებას Y = a0 + b1X1 სახით, ეს არის წრფივი რეგრესიის მოდელი. თუ არა, ის არაწრფივია. Y = f(X,β) + ε X = p პროგნოზირების ვექტორი, β = k პარამეტრების ვექტორი, f(-) = ცნობილი რეგრესიული ფუნქცია, ε = შეცდომის ვადა
რა არის დამხმარე რეგრესია?
დამხმარე რეგრესია: რეგრესია, რომელიც გამოიყენება ტესტის სტატისტიკის გამოსათვლელად - როგორიცაა ტესტის სტატისტიკა ჰეტეროსკედასტიურობისა და სერიული კორელაციისთვის ან ნებისმიერი სხვა რეგრესია, რომელიც არ აფასებს პირველადი ინტერესის მოდელს
როგორ გამოვთვალოთ სინუსოიდური რეგრესია?
სინუსოიდური რეგრესია. დაარეგულირეთ A, B, C და D მნიშვნელობები y = A*sin(B(x-C))+D განტოლებაში, რათა სინუსოიდური მრუდი მოერგოს შემთხვევით გენერირებულ მონაცემებს. კარგი ფუნქცია რომ გექნებათ, დააწკაპუნეთ „გამოთვლილი ჩვენება“გამოთვლილი რეგრესიის ხაზის სანახავად. გამოიყენეთ 'ctr-R' ახალი მონაცემთა წერტილების შესაქმნელად და ხელახლა სცადეთ
