ვიდეო: რა არის ექსპონენციალური და ლოგარითმული ფუნქციები?
2024 ავტორი: Miles Stephen | [email protected]. ბოლოს შეცვლილი: 2023-12-15 23:37
ლოგარითმული ფუნქციები არის შებრუნებული ექსპონენციალური ფუნქციები . -ის ინვერსია ექსპონენციალური ფუნქცია y = ax არის x = aწ. The ლოგარითმული ფუნქცია y = ჟურნალიაx განისაზღვრება, როგორც ექვივალენტური ექსპონენციალური განტოლება x = aწ. y = ჟურნალიაx მხოლოდ შემდეგ პირობებში: x = aწ, a > 0 და a≠1.
შესაბამისად, რა განსხვავებაა ექსპონენციალურ და ლოგარითმულ ფუნქციებს შორის?
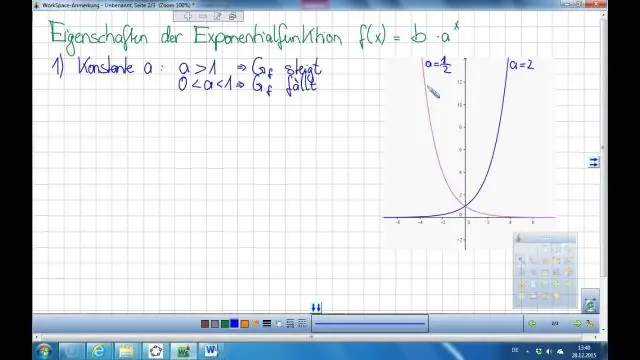
შებრუნებული ა ექსპონენციალური ფუნქცია არის ლოგარითმული ფუნქცია და ა-ს შებრუნებული ლოგარითმული ფუნქცია არის ექსპონენციალური ფუნქცია . ასევე შენიშნეთ გრაფიკზე, რომ რაც უფრო დიდი და დიდი ხდება x, ის ფუნქცია f(x)-ის მნიშვნელობა სულ უფრო და უფრო მკვეთრად იზრდება.
რა არის ლოგარითმული ფუნქციის მაგალითი? ა ლოგარითმი არის ექსპონენტი. ნებისმიერი ექსპონენციალური გამოხატულება შეიძლება გადაიწეროს ლოგარითმული ფორმა. ამისთვის მაგალითი , თუ გვაქვს 8 = 23, მაშინ საფუძველი არის 2, მაჩვენებელი არის 3 და შედეგი არის 8. ეს შეიძლება გადაიწეროს ლოგარითმული ფორმა როგორც. 3 = ჟურნალი 2 8.
ამასთან დაკავშირებით, რა არის ექსპონენციალური ლოგარითმი?
Განმარტებით: ჟურნალი ბy = x ნიშნავს b x = y. შეესაბამება ყოველი ლოგარითმი ფუნქცია b ფუძით, ჩვენ ვხედავთ, რომ არსებობს an ექსპონენციალური ფუნქცია b ფუძით: y = b x. ან ექსპონენციალური ფუნქცია არის a-ს შებრუნებული ლოგარითმი ფუნქცია.
რა არის ექსპონენციალური ფუნქციის მაგალითი?
ში ექსპონენციალური ფუნქცია დამოუკიდებელი ცვლადი, ან x-მნიშვნელობა არის ექსპონენტი , ხოლო ფუძე არის მუდმივი. ამისთვის მაგალითი , y = 2x იქნება an ექსპონენციალური ფუნქცია . აი, როგორ გამოიყურება. ფორმულა ა ექსპონენციალური ფუნქცია არის y = abx, სადაც a და b მუდმივებია.
გირჩევთ:
რა არის ექსპონენციალური ფუნქციის შებრუნებული?
Y = ax ექსპონენციალური ფუნქციის შებრუნებული არის x = ay. ლოგარითმული ფუნქცია y = ლოგაქსი განისაზღვრება ექსპონენციალური განტოლების ექვივალენტად x = ay
რა არის ექსპონენციალური აზროვნება?
იფიქრე ექსპონენტურად. ექსპონენციალური აზროვნება არსებობს იმის შესაცვლელად, თუ როგორ ხედავთ ტექნოლოგიას - მასზე ფიქრი, როგორც პროგნოზირებადი ნაბიჯების ან თაობების სერია. შედეგები იცვლება სამყაროში. ადამიანები ფიქრობენ იმ ტერმინებით, რომელთანაც შეუძლიათ ურთიერთობა. ჩვენ ჩვენს მოლოდინებს ვაფუძნებთ ჩვენს გამოცდილებას, ვცხოვრობთ წრფივ დროსა და სივრცეში
როგორ არის მსგავსი ექსპონენციალური და ლოგისტიკური ფუნქციები?
მოსახლეობის ექსპონენციალური ზრდა: როდესაც რესურსები შეუზღუდავია, პოპულაციები აჩვენებენ ექსპონენციალურ ზრდას, რის შედეგადაც წარმოიქმნება J- ფორმის მრუდი. როდესაც რესურსები შეზღუდულია, მოსახლეობა ავლენს ლოგისტიკურ ზრდას. ლოგისტიკური ზრდის დროს, მოსახლეობის გაფართოება მცირდება, რადგან რესურსები მწირი ხდება
რა არის მოსახლეობის ექსპონენციალური ზრდა ბიოლოგიაში?
ბიოლოგიური ექსპონენციალური ზრდა არის ბიოლოგიური ორგანიზმების ექსპონენციალური ზრდა. როდესაც რესურსების ხელმისაწვდომობა შეუზღუდავია ჰაბიტატში, ჰაბიტატში მცხოვრები ორგანიზმის პოპულაცია ექსპონენციურად ან გეომეტრიულად იზრდება. სხვა სიტყვებით რომ ვთქვათ, მოსახლეობა ექსპონენტურ ზრდას განიცდის
როგორ გამოვსახოთ ლოგარითმული ფუნქციები კალკულატორზე?
გრაფიკული კალკულატორზე ბაზის e ლოგარითმი არის ln გასაღები. სამივე ერთნაირია. თუ თქვენ გაქვთ logBASE ფუნქცია, ის შეიძლება გამოყენებულ იქნას ფუნქციის შესაყვანად (იხილეთ Y1 ქვემოთ). თუ არა, გამოიყენეთ Change of Base ფორმულა (იხილეთ Y2 ქვემოთ)