
- ავტორი Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:37.
- ბოლოს შეცვლილი 2025-01-22 17:03.
რეგრესია არის უპირველეს ყოვლისა ხოლმე მოდელების/განტოლებების აგება რომ იწინასწარმეტყველეთ საკვანძო პასუხი, Y, პროგნოზირების (X) ცვლადების სიმრავლიდან. კორელაცია არის უპირველეს ყოვლისა ხოლმე სწრაფად და მოკლედ შეაჯამეთ 2 ან მეტი რიცხვითი ცვლადის სიმრავლეს შორის ურთიერთობების მიმართულება და ძალა.
ასევე უნდა იცოდეთ, როდის უნდა გამოიყენოთ წრფივი რეგრესია?
სამი ძირითადი იყენებს ამისთვის რეგრესია ანალიზი არის (1) პროგნოზირების სიძლიერის განსაზღვრა, (2) ეფექტის პროგნოზირება და (3) ტენდენციის პროგნოზირება. პირველი, რეგრესია შეიძლება გამოყენებულ იქნას რომ დამოუკიდებელ ცვლად(ებ)ს დამოკიდებულ ცვლადზე მოქმედების სიძლიერის განსაზღვრა.
ასევე, როდის უნდა იქნას გამოყენებული კორელაცია? კორელაცია არის გამოყენებული ორ უწყვეტ ცვლადს (მაგ. სიმაღლე და წონა) შორის წრფივი ურთიერთობის აღსაწერად. Ზოგადად, კორელაცია მიდრეკილია იყოს გამოყენებული როდესაც არ არის გამოვლენილი პასუხის ცვლადი. ის ზომავს ორ ან მეტ ცვლადს შორის წრფივი ურთიერთობის სიძლიერეს (ხარისხობრივად) და მიმართულებას.
შეიძლება ასევე იკითხოს, რა განსხვავებაა მარტივ წრფივ რეგრესიასა და კორელაციას შორის?
რეგრესია აღწერს, თუ როგორ არის დამოუკიდებელი ცვლადი რიცხობრივად დაკავშირებული დამოკიდებულ ცვლადთან. კორელაცია გამოიყენება წარმოსაჩენად ხაზოვანი ურთიერთობა შორის ორი ცვლადი. Საპირისპიროდ, რეგრესია გამოიყენება საუკეთესო სტრიქონისთვის და ერთი ცვლადის შესაფასებლად დან სხვა ცვლადი.
რა არის მართალი პირსონის კორელაციასა და მარტივ წრფივ რეგრესიაზე?
პირსონის კორელაცია და ხაზოვანი რეგრესია . ა კორელაცია ანალიზი იძლევა ინფორმაციას სიძლიერისა და მიმართულების შესახებ ხაზოვანი ურთიერთობა ორ ცვლადს შორის, ხოლო ა მარტივი ხაზოვანი რეგრესიული ანალიზი აფასებს პარამეტრებს ა ხაზოვანი განტოლება, რომელიც შეიძლება გამოყენებულ იქნას ერთი ცვლადის მნიშვნელობების პროგნოზირებისთვის მეორეზე დაყრდნობით
გირჩევთ:
რა არის უარყოფითი წრფივი კორელაცია?

უარყოფითი კორელაცია ნიშნავს, რომ ორ ცვლადს შორის არის საპირისპირო კავშირი - როდესაც ერთი ცვლადი მცირდება, მეორე იზრდება
როგორ არის მსგავსი წრფივი უტოლობებისა და წრფივი განტოლებების ამოხსნა?

წრფივი უტოლობების ამოხსნა ძალიან ჰგავს წრფივი განტოლებების ამოხსნას. მთავარი განსხვავება ისაა, რომ თქვენ აბრუნებთ უტოლობის ნიშანს უარყოფით რიცხვზე გაყოფისას ან გამრავლებისას. წრფივი უტოლობების გრაფიკას კიდევ რამდენიმე განსხვავება აქვს. ნაწილი, რომელიც დაჩრდილულია, მოიცავს მნიშვნელობებს, სადაც წრფივი უტოლობა არის ჭეშმარიტი
როდის უნდა გამოვიყენო ანოვა?

როგორც წესი, ცალმხრივი ANOVA გამოიყენება, როდესაც გაქვთ სამი ან მეტი კატეგორიული, დამოუკიდებელი ჯგუფი, მაგრამ ის შეიძლება გამოყენებულ იქნას მხოლოდ ორი ჯგუფისთვის (მაგრამ დამოუკიდებელი ნიმუშის t-ტესტი უფრო ხშირად გამოიყენება ორი ჯგუფისთვის)
რა არის წრფივი პროგრამირების მარტივი მეთოდი?
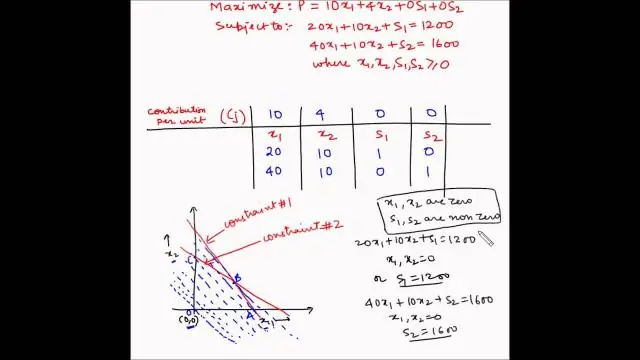
მარტივი მეთოდი. მარტივი მეთოდი, სტანდარტული ტექნიკა წრფივ პროგრამირებაში ოპტიმიზაციის პრობლემის გადასაჭრელად, რომელიც ჩვეულებრივ მოიცავს ფუნქციას და უტოლობად გამოხატულ რამდენიმე შეზღუდვას. უტოლობები განსაზღვრავენ მრავალკუთხედს (იხ. მრავალკუთხედი) და ამონახსნი ჩვეულებრივ ერთ-ერთ წვეროზეა
როდის შეიძლება გამოვიყენოთ გამოყოფის აორთქლების მეთოდი?

აორთქლება არის ტექნიკა, რომელიც გამოიყენება ერთგვაროვანი ნარევების გამოსაყოფად, სადაც არის ერთი ან მეტი გახსნილი მარილი. მეთოდი აშორებს თხევად კომპონენტებს მყარი კომპონენტებისგან. პროცესი, როგორც წესი, მოიცავს ნარევის გაცხელებას, სანამ სითხე აღარ დარჩება
