ვიდეო: რა არის იდენტობის კანონი დისკრეტულ მათემატიკაში?
2024 ავტორი: Miles Stephen | [email protected]. ბოლოს შეცვლილი: 2023-12-15 23:37
ასე რომ პირადობის კანონი , p∧T≡p, ნიშნავს, რომ ნებისმიერი p წინადადების კავშირს თვითნებურ ტავტოლოგიასთან T ყოველთვის ექნება იგივე ჭეშმარიტების მნიშვნელობა, როგორც p (ე.ი. ლოგიკურად იქნება p-ის ექვივალენტი). ეს ნიშნავს, რომ ნებისმიერი p წინადადების განცალკევება თვითნებურ ტავტოლოგიასთან T ყოველთვის იქნება ჭეშმარიტი (თვითონ იქნება ტავტოლოგია).
ასევე უნდა იცოდეთ, რა არის იდენტობის კანონი მათემატიკაში?
ან ვინაობა არის თანასწორობა, რომელიც მართებულია მისი ცვლადების არჩეული მნიშვნელობების მიუხედავად. მაგალითად, ვინაობა (x + y) 2 = x 2 + 2 xy + y 2 (x+y)^2 = x^2 + 2xy + y^2 (x+y)2=x2+2xy+y2 მართალია ყველა არჩევანისთვის x და y, რეალური თუ რთული რიცხვები.
გარდა ამისა, რა არის იდენტობის პრინციპის მაგალითი? ლოგიკაში კანონი ვინაობა აცხადებს, რომ თითოეული ნივთი თავისთავად იდენტურია. ეს არის აზროვნების სამი კანონიდან პირველი, შეუსაბამობის კანონთან ერთად და გამორიცხული შუალედური კანონით. ის ასევე შეიძლება დაიწეროს ნაკლებად ფორმალურად, როგორც A არის A. ასეთი a-ს ერთი განცხადება პრინციპი არის "ვარდი ვარდი ვარდი ვარდი ვარდია."
შემდგომში შეიძლება ისიც იკითხოს, რა არის დე მორგანის კანონი დისკრეტულ მათემატიკაში?
დე მორგანის კანონები აღწერეთ როგორ მათემატიკური განცხადებები და ცნებები დაკავშირებულია მათი საპირისპიროებით. სიმრავლეების თეორიაში, დე მორგანის კანონები დააკავშიროს სიმრავლეების გადაკვეთა და გაერთიანება კომპლემენტების მეშვეობით. წინადადების ლოგიკაში, დე მორგანის კანონები წინადადებების კავშირებისა და განცალკევების დაკავშირება უარყოფის გზით.
რა არის დისკრეტული მათემატიკის შედეგები?
განმარტება: მოდით, p და q იყოს წინადადებები. წინადადება "p ან q", რომელიც აღინიშნება p ∨ q-ით, მცდარია, როდესაც ორივე p და q მცდარია და სხვაგვარად მართალია. p → q-ით აღნიშნულ წინადადებას „p გულისხმობს q“ეწოდება იმპლიკამენტი . მცდარია, როდესაც p არის ჭეშმარიტი და q არის მცდარი და მართალია სხვაგვარად.
გირჩევთ:
რატომ არის დალტონის კანონი შემზღუდველი კანონი?
დალტონის კანონის შეზღუდვა კანონი კარგად მოქმედებს რეალურ გაზებზე დაბალ წნევაზე, მაგრამ მაღალი წნევის დროს ის მნიშვნელოვნად გადახრის. აირების ნარევი ბუნებით არარეაქტიულია. ასევე ვარაუდობენ, რომ თითოეული ცალკეული აირის მოლეკულებს შორის ურთიერთქმედება იგივეა, რაც ნარევის მოლეკულებს
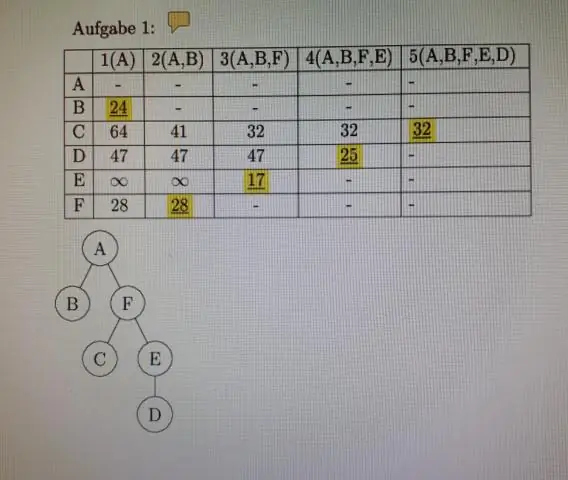
რა არის მატრიცები დისკრეტულ მათემატიკაში?
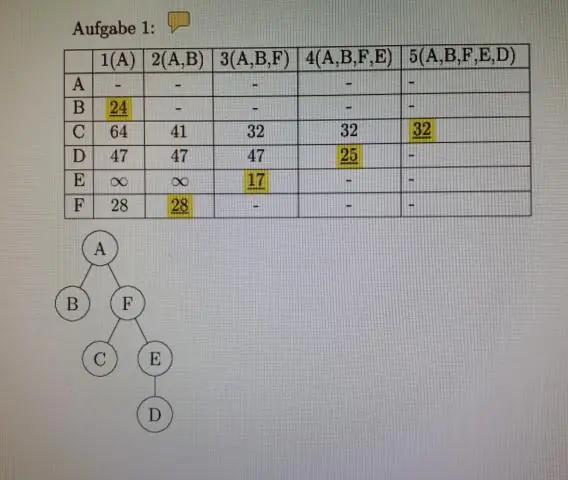
დისკრეტული მათემატიკა და მისი აპლიკაციები თავი2 შენიშვნები 2.6 მატრიცების ლექციის სლაიდები Adil Aslammailto:[email protected]. მატრიქსის განმარტება •მატრიცა არის რიცხვების მართკუთხა მასივი. მატრიქსის m რიგები და n სვეტი ეწოდება m x n მატრიცას. მატრიცის მრავლობითი არის მატრიცები
რა არის მასის შენარჩუნების კანონი და რატომ არის ის მნიშვნელოვანი?
მასის შენარჩუნების კანონი ძალზე მნიშვნელოვანია ქიმიური რეაქციების შესწავლისა და წარმოებისთვის. თუ მეცნიერებმა იციან რეაგენტების რაოდენობა და ვინაობა კონკრეტული რეაქციისთვის, მათ შეუძლიათ წინასწარ განსაზღვრონ წარმოებული პროდუქტების რაოდენობა
როგორ პოულობთ უწყვეტ და დისკრეტულ მონაცემებს?
მარტივი სიტყვებით, დისკრეტული მონაცემები ითვლიან და უწყვეტი მონაცემები იზომება. დისკრეტული მონაცემების მაგალითები იქნება ძაღლების რაოდენობა, სტუდენტების რაოდენობა ან ფულის ოდენობა. უწყვეტი მონაცემები შეიძლება იყოს ძაღლების სიმაღლე ან წონა, ან მილის გაშვებისთვის საჭირო დრო
რა არის ეკვივალენტობა დისკრეტულ მათემატიკაში?
მათემატიკაში ეკვივალენტურობის მიმართება არის ორობითი მიმართება, რომელიც არის რეფლექსური, სიმეტრიული და გარდამავალი. მიმართება „ტოლია“არის ეკვივალენტური მიმართების კანონიკური მაგალითი, სადაც a, b და c ობიექტებისთვის: a = a (რეფლექსური თვისება), თუ a = b და b = c, მაშინ a = c (გარდამავალი თვისება )