Სარჩევი:
ვიდეო: როგორ ამრავლებთ კომპოზიციურ ფუნქციებს?
2024 ავტორი: Miles Stephen | [email protected]. ბოლოს შეცვლილი: 2023-12-15 23:37
გამრავლება და ფუნქციების შედგენა
- რომ გამრავლება ა ფუნქცია სკალარით, გამრავლება თითოეული გამომავალი ამ სკალარის მიერ.
- როდესაც ვიღებთ f (g(x)), ვიღებთ g(x)-ს, როგორც შეყვანა ფუნქცია ვ.
- მაგალითად, თუ f (x) = 10x და g(x) = x + 1, მაშინ f (g(4)) საპოვნელად ვპოულობთ g(4) = 4 + 1 + 5 და შემდეგ შევაფასებთ f (5)) = 10(5) = 50.
- მაგალითი: f (x) = 2x - 2, g(x) = x2 - 8.
შესაბამისად, როგორ ასრულებთ მრავალ ფუნქციას?
გამრავლება ფუნქციები რომ გამრავლება ა ფუნქცია სხვის მიერ ფუნქცია , გამრავლება მათი შედეგები. მაგალითად, თუ f (x) = 2x და g(x) = x + 1, მაშინ fg(3) = f (3)×g(3) = 6×4 = 24. fg(x) = 2x(x + 1) = 2x2 + x.
გარდა ამისა, როგორ ასახავთ ფუნქციას? განიხილეთ ფუნქცია f(x) = 2 x + 1. ჩვენ ვაღიარებთ განტოლებას y = 2 x + 1, როგორც წრფის განტოლების Slope-Intercept ფორმა 2 დახრილობით და y-კვეთა (0, 1). იფიქრეთ იმაზე, რომ მოძრაობს წერტილი გრაფიკი ვ-ის როდესაც წერტილი მოძრაობს მარჯვნივ, ის იზრდება.
შემდგომში შეიძლება ისიც იკითხოს, რა არის ორი ფუნქციის პროდუქტი?
როცა ამრავლებ ორი ფუნქცია ერთად, თქვენ მიიღებთ მესამედს ფუნქცია შედეგად და ის მესამე ფუნქცია იქნება პროდუქტი საქართველოს ორი ორიგინალური ფუნქციები . მაგალითად, თუ გაამრავლებთ f(x) და g(x), მათი პროდუქტი იქნება h(x)=fg(x), ან h(x)=f(x)g(x). თქვენ ასევე შეგიძლიათ შეაფასოთ პროდუქტი კონკრეტულ მომენტში.
როგორ ამოხსნით ფუნქციას?
ამისთვის ფუნქციები , ორი აღნიშვნა ზუსტად ერთსა და იმავეს ნიშნავს, მაგრამ "f (x)" გაძლევთ მეტ მოქნილობას და მეტ ინფორმაციას. თქვენ ამბობდით "y = 2x + 3; გადაჭრა y-სთვის, როდესაც x = –1". ახლა თქვენ თქვით "f (x) = 2x + 3; იპოვეთ f (–1)" (გამოითქმის როგორც "f-of-x უდრის 2x-ს პლუს სამი; იპოვეთ f-of-უარყოფითი-ერთი").
გირჩევთ:
როგორ აფასებთ კომპოზიციურ ფუნქციებს?
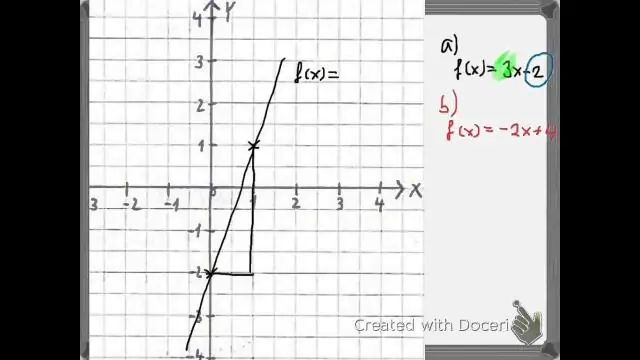
კომპოზიტური ფუნქციების შეფასება გრაფიკების გამოყენებით იპოვნეთ შიდა ფუნქციის მოცემული შეყვანა მისი გრაფიკის x ღერძზე. წაიკითხეთ შიდა ფუნქციის გამოსავალი მისი გრაფიკის y ღერძიდან. იპოვნეთ შიდა ფუნქციის გამოსავალი გარე ფუნქციის გრაფიკის x ღერძზე
როგორ პოულობთ რკალი ტრიგის ფუნქციებს?
შებრუნებულ ფუნქციას აღვნიშნავთ როგორც y=sin−1(x). იკითხება y არის სინუს x-ის შებრუნებული და ნიშნავს y არის რეალური რიცხვის კუთხე, რომლის სინუს მნიშვნელობა არის x. ფრთხილად იყავით გამოყენებული აღნიშვნით. შებრუნებული ტრიგონომეტრიული ფუნქციების გრაფიკები. ფუნქცია დომენის დიაპაზონი csc&მინუს;1(x) (&მინუს;∞,&მინუს;1]&თასი;[1,∞) [&მინუს;π2,0)&თასი;(0,π2]
რატომ უწოდებენ ტრიგონომეტრიულ ფუნქციებს წრიულ ფუნქციებს?
ტრიგონომეტრიულ ფუნქციებს ზოგჯერ წრიულ ფუნქციებსაც უწოდებენ. ეს იმიტომ ხდება, რომ ორი ფუნდამენტური ტრიგონომეტრიული ფუნქცია - სინუსი და კოსინუსი - განისაზღვრება, როგორც P წერტილის კოორდინატები, რომელიც მოძრაობს რადიუსის 1-ის ერთეული წრის გარშემო. სინუსი და კოსინუსი იმეორებენ თავიანთ გამოსავალს რეგულარული ინტერვალებით
როგორ გარდაქმნით წრფივ ფუნქციებს?
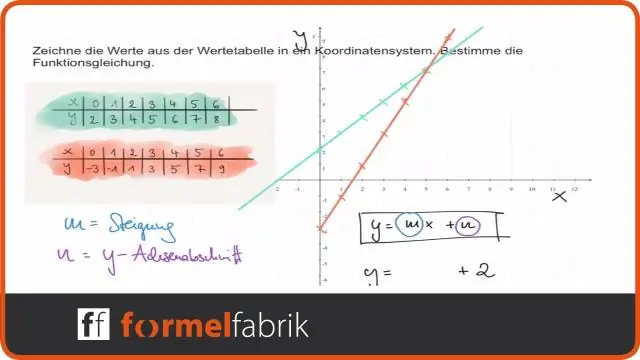
როგორ: წრფივი ფუნქციის განტოლებიდან გამომდინარე, გამოიყენეთ გარდაქმნები წრფივი ფუნქციის გრაფიკისთვის f(x)=mx+b f (x) = m x + b. გრაფიკი f(x)=x f (x) = x. ვერტიკალურად გაჭიმეთ ან შეკუმშეთ გრაფიკი |m| ფაქტორით. გადაიტანეთ გრაფიკი ზევით ან ქვევით b ერთეულებით
როგორ ამრავლებთ რაციონალურ ფუნქციებს?
Q და S არ უდრის 0-ს. ნაბიჯი 1: შეადარეთ როგორც მრიცხველი, ასევე მნიშვნელი. ნაბიჯი 2: ჩაწერეთ როგორც ერთი წილადი. ნაბიჯი 3: რაციონალური გამოხატვის გამარტივება. ნაბიჯი 4: გაამრავლეთ დარჩენილი ფაქტორები მრიცხველში და/ან მნიშვნელში. ნაბიჯი 1: შეაფასეთ როგორც მრიცხველი, ასევე მნიშვნელი. ნაბიჯი 2: ჩაწერეთ როგორც ერთი წილადი