
- ავტორი Miles Stephen [email protected].
- Public 2023-12-15 23:37.
- ბოლოს შეცვლილი 2025-06-01 05:04.
ჩვენ აღვნიშნავთ შებრუნებული ფუნქცია როგორც y=sin−1(x). იკითხება y არის შებრუნებული დან სინუსური x და ნიშნავს y არის რეალური რიცხვის კუთხე რომლის სინუსური მნიშვნელობა არის x. ფრთხილად იყავით გამოყენებული აღნიშვნით.
გრაფიკები შებრუნებული ტრიგონომეტრიული ფუნქციები.
| ფუნქცია | დომენი | Დიაპაზონი |
|---|---|---|
| csc−1(x) | (−∞, −1]∪[1, ∞) | [−π2, 0)∪(0, π2] |
შემდგომში, შეიძლება ასევე იკითხოთ, როგორ პოულობთ ARC ფუნქციას?
Შენ იყენებ შებრუნებული ტრიგონომეტრია ფუნქციები განტოლებების ამოსახსნელად, როგორიცაა sin x = 1/2, sec x = -2, ან tan 2x = 1. ტიპიურ ალგებრის განტოლებებში, თქვენ შეგიძლიათ ამოხსნათ x-ის მნიშვნელობა განტოლების თითოეული მხარის გაყოფით ცვლადის კოეფიციენტზე. ან თითოეულ მხარეს ერთი და იგივე ნივთის მიმატებით და ა.შ.
მეორეც, რა არის რკალი ცოდვა? არქსინი განმარტება x-ის რკალი განისაზღვრება, როგორც x-ის ინვერსიული სინუსური ფუნქცია, როდესაც -1≦x≦1. როცა y-ის სინუსი x-ის ტოლია: sin y = x. მაშინ x-ის რკალი უდრის x-ის შებრუნებულ სინუს ფუნქციას, რომელიც უდრის y-ს: რკალი x = ცოდვა-1 x = y.
ასევე კითხვაა, რა არის ცოდვის საპირისპირო?
ცოდვის ფუნქციის ინვერსია არის arcsin ფუნქცია. მაგრამ სინუსური თავისთავად, არ იქნება შექცევადი, რადგან ის არ არის ინექციური, ამიტომ არ არის ორმხრივი (შებრუნებული). arcsine ფუნქციის მისაღებად ჩვენ უნდა შევზღუდოთ დომენი სინუსური [−π2, π2]-მდე.
რა არის Sinhx?
Sinh(α) არის ჰიპერბოლური სინუსი. მაშინ როცა ტრიგონომეტრიული Sin(α) არის პერპენდიკულარულის სიგრძე, რომელიც ჩამოშვებულია ერთეული წრის წერტილიდან (წრის რადიუსი = 1) x ღერძზე α კუთხისთვის.
გირჩევთ:
როგორ აფასებთ კომპოზიციურ ფუნქციებს?
კომპოზიტური ფუნქციების შეფასება გრაფიკების გამოყენებით იპოვნეთ შიდა ფუნქციის მოცემული შეყვანა მისი გრაფიკის x ღერძზე. წაიკითხეთ შიდა ფუნქციის გამოსავალი მისი გრაფიკის y ღერძიდან. იპოვნეთ შიდა ფუნქციის გამოსავალი გარე ფუნქციის გრაფიკის x ღერძზე
როგორ ამრავლებთ კომპოზიციურ ფუნქციებს?

ფუნქციების გამრავლება და შედგენა ფუნქციის სკალარზე გასამრავლებლად, თითოეული გამომავალი გავამრავლოთ ამ სკალარზე. როდესაც ვიღებთ f (g(x)), ვიღებთ g(x)-ს, როგორც f ფუნქციის შეყვანა. მაგალითად, თუ f (x) = 10x და g(x) = x + 1, მაშინ f (g(4)) საპოვნელად ვპოულობთ g(4) = 4 + 1 + 5 და შემდეგ შევაფასებთ f (5) ) = 10(5) = 50. მაგალითი: f (x) = 2x - 2, g(x) = x2 - 8
რატომ უწოდებენ ტრიგონომეტრიულ ფუნქციებს წრიულ ფუნქციებს?

ტრიგონომეტრიულ ფუნქციებს ზოგჯერ წრიულ ფუნქციებსაც უწოდებენ. ეს იმიტომ ხდება, რომ ორი ფუნდამენტური ტრიგონომეტრიული ფუნქცია - სინუსი და კოსინუსი - განისაზღვრება, როგორც P წერტილის კოორდინატები, რომელიც მოძრაობს რადიუსის 1-ის ერთეული წრის გარშემო. სინუსი და კოსინუსი იმეორებენ თავიანთ გამოსავალს რეგულარული ინტერვალებით
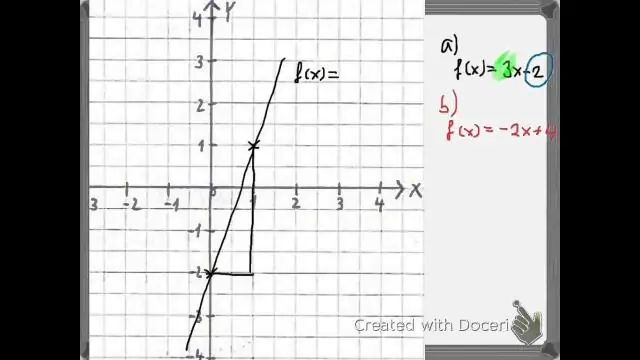
როგორ გარდაქმნით წრფივ ფუნქციებს?
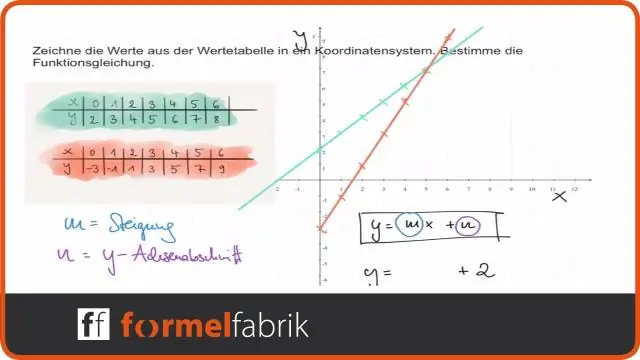
როგორ: წრფივი ფუნქციის განტოლებიდან გამომდინარე, გამოიყენეთ გარდაქმნები წრფივი ფუნქციის გრაფიკისთვის f(x)=mx+b f (x) = m x + b. გრაფიკი f(x)=x f (x) = x. ვერტიკალურად გაჭიმეთ ან შეკუმშეთ გრაფიკი |m| ფაქტორით. გადაიტანეთ გრაფიკი ზევით ან ქვევით b ერთეულებით
როგორ ამოხსნით აბსოლუტურ ფუნქციებს?
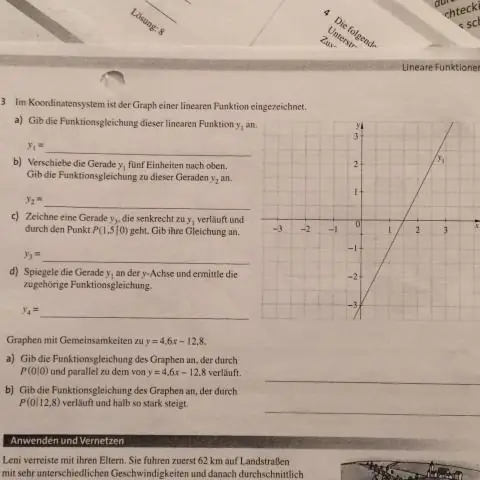
აბსოლუტური სიდიდე(ებ)ის შემცველი განტოლების ამოხსნა ნაბიჯი 1: გამოყავით აბსოლუტური მნიშვნელობის გამოხატულება. ნაბიჯი 2: დააყენეთ რაოდენობა აბსოლუტური მნიშვნელობის აღნიშვნის ტოლი + და - რაოდენობის განტოლების მეორე მხარეს. ნაბიჯი 3: ამოხსენით უცნობი ორივე განტოლებაში. ნაბიჯი 4: შეამოწმეთ თქვენი პასუხი ანალიტიკურად ან გრაფიკულად
