
- ავტორი Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:37.
- ბოლოს შეცვლილი 2025-01-22 17:03.
ურთიერთგამომრიცხავი მოვლენები არ შეიძლება მოხდეს იმავე დროს . მაგალითად: მონეტის სროლისას შედეგი შეუძლია იყოს თავები ან კუდები, მაგრამ არ შეიძლება იყოს ორივე . ეს რა თქმა უნდა ნიშნავს ურთიერთგამომრიცხავი მოვლენები არ არის დამოუკიდებელი , და დამოუკიდებელი ღონისძიებები შეუძლებელია იყოს ურთიერთგამომრიცხავი . ( Ივენთი ნულოვანი ზომის გამოკლებით.)
ამის გათვალისწინებით, შესაძლებელია თუ არა დამოუკიდებელი მოვლენები ერთდროულად მოხდეს?
გაითვალისწინეთ, რომ განცალკევება მოვლენები და დამოუკიდებელი ღონისძიებები განსხვავებულები არიან. Ივენთი განიხილება განცალკევებით, თუ ისინი არასდროს მოხდეს ამავე დროს ; ეს ასევე ცნობილია როგორც ურთიერთგამომრიცხავი ივენთი . Ივენთი განიხილება დამოუკიდებელი თუ ისინი არ არიან დაკავშირებული. ორი ივენთი რომ კეთება არა მოხდეს ამავე დროს.
ანალოგიურად, შეიძლება თუ არა ორი მოვლენა იყოს არაერთგვაროვანი და დამოუკიდებელი? ორი განსხვავებული მოვლენა შეიძლება არასდროს იყო დამოუკიდებელი , გარდა იმ შემთხვევისა, როდესაც ერთ-ერთი ივენთი არის ნულოვანი. Ივენთი განიხილება დაშლილი თუ ისინი არასოდეს ხდებიან ერთდროულად. მაგალითად, პირველკურსელი და მეორე კურსის სტუდენტობა ჩაითვლება განუყოფელი მოვლენები . დამოუკიდებელი მოვლენები არ არიან დაკავშირებული ივენთი.
უბრალოდ, ორი ურთიერთგამომრიცხავი არანულოვანი მოვლენა ასევე დამოუკიდებელზეა დამოკიდებული თუ?
ორი მოვლენა თან ნულოვანი ალბათობა არ შეიძლება იყოს ორივე ურთიერთგამომრიცხავი და დამოუკიდებელი . თუ ერთი ურთიერთგამომრიცხავი ღონისძიება ცნობილია, რომ ხდება, მეორე არ შეიძლება მოხდეს.; ამრიგად, მეორეს ალბათობა ღონისძიება მომხდარი მცირდება ნული (და ამიტომ არიან დამოკიდებული ).
როგორ იცით, არის თუ არა ღონისძიება დამოუკიდებელი?
შესამოწმებლად თუ არა ორი ივენთი A და B არიან დამოუკიდებელი , გამოთვალეთ P(A), P(B) და P(A ∩ B) და შემდეგ შეამოწმეთ თუ არა P(A ∩ B) უდრის P(A)P(B). თუ ისინი ტოლია, A და B არის დამოუკიდებელი ; თუ არა, ისინი დამოკიდებულნი არიან.
გირჩევთ:
რა არის დამოუკიდებელი მოვლენა ალბათობით?

დამოუკიდებელი მოვლენები. როდესაც ნათქვამია, რომ ორი მოვლენა ერთმანეთისგან დამოუკიდებელია, ეს ნიშნავს, რომ ერთი მოვლენის დადგომის ალბათობა არანაირად არ მოქმედებს მეორე მოვლენის დადგომის ალბათობაზე. ორი დამოუკიდებელი მოვლენის მაგალითი შემდეგია; თქვით, რომ თქვენ შემოახვიეთ კუპიურა და გადაატრიალეთ მონეტა
შეიძლება თუ არა ჩი კვადრატი იყოს უარყოფითი?
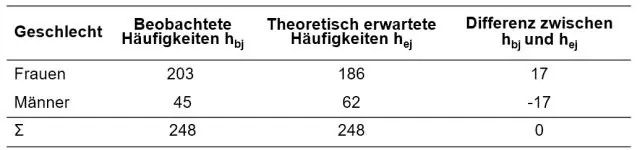
გულისხმობთ: შეიძლება თუ არა ჩი კვადრატის მნიშვნელობები უარყოფითი იყოს? პასუხი არის არა. ჩი კვადრატის მნიშვნელობა არ შეიძლება იყოს უარყოფითი, რადგან ის ეფუძნება კვადრატული განსხვავებების ჯამს (მიღებულ და მოსალოდნელ შედეგებს შორის)
შეიძლება თუ არა უარყოფითი და დადებითი ფერდობები იყოს პარალელური?

თეორემა 104: თუ ორ წრფეს აქვს ერთი და იგივე დახრილობა, მაშინ წრფეები არავერტიკალური პარალელური ხაზებია. თუ ორი ხაზი პერპენდიკულარულია და არც ერთი არ არის ვერტიკალური, მაშინ ერთ წრფეს აქვს დადებითი დახრილობა, ხოლო მეორეს აქვს უარყოფითი დახრილობა. ასევე, მათი ფერდობების აბსოლუტური მნიშვნელობები ორმხრივია
შეიძლება იყოს თუ არა ორი წრფივი განტოლების გრაფიკებს შორის გადაკვეთის ერთზე მეტი წერტილი?

თუ ორი წრფივი განტოლების გრაფიკები არ ემთხვევა, შეიძლება იყოს მხოლოდ ერთი გადაკვეთის წერტილი, რადგან ორი წრფე შეიძლება იკვეთოს მაქსიმუმ ერთ წერტილში. ამ წერტილიდან გადაიტანეთ ერთი ერთეული მარჯვნივ და ვერტიკალურად გადაიტანეთ ფერდობის მნიშვნელობა მეორე წერტილის გამოსათვლელად. შემდეგ დააკავშირეთ ორი წერტილი
შეუძლია თუ არა დედამიწაზე ყველას ერთდროულად ნახოს მთვარე?

დედამიწის ზედაპირის დაახლოებით მესამედს შეუძლია მთვარის დანახვა ნებისმიერ დროს, ან ნახევარი, თუ მთვარე ჰორიზონტიდან ჰორიზონტამდეა დანახული. ყველა ხედავს მთვარეს სხვადასხვა პოზიციებზე ერთდროულად დედამიწის დაახლოებით ნახევარიდან
